Corrispondenze e Relazioni
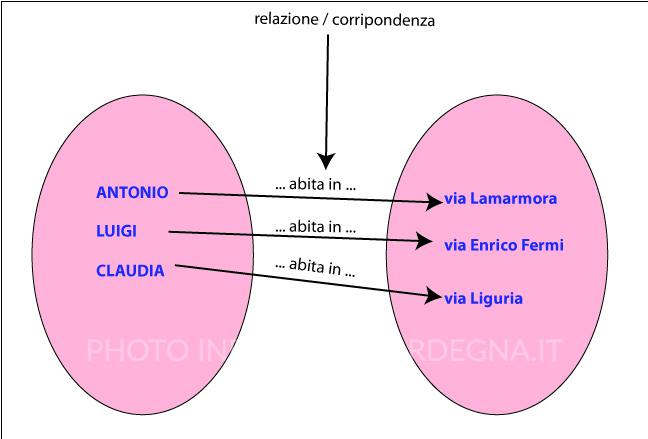
Ogni elemento dell’insieme A è in relazione (o in corrispondenza) con un ben determinato elemento dell’insieme B.
- La relazione è stabilita dalle parole «… abita in …»
- La relazione è una corrispondenza
La corrispondenza può essere:
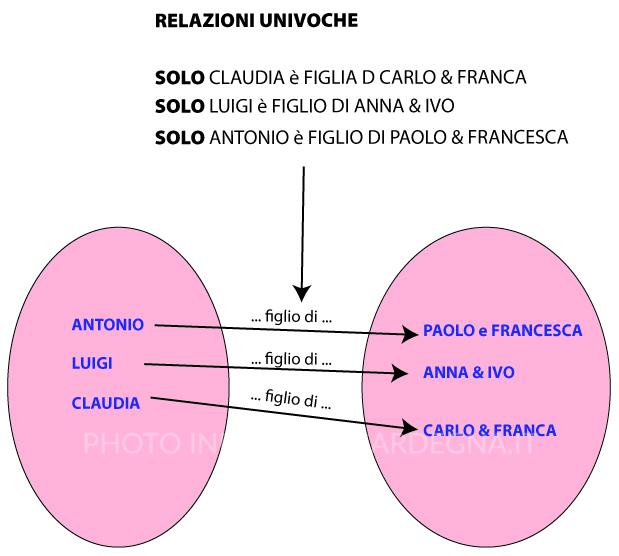
- corrispondenza univoca – Solo Antonio abita in via Lamarmora
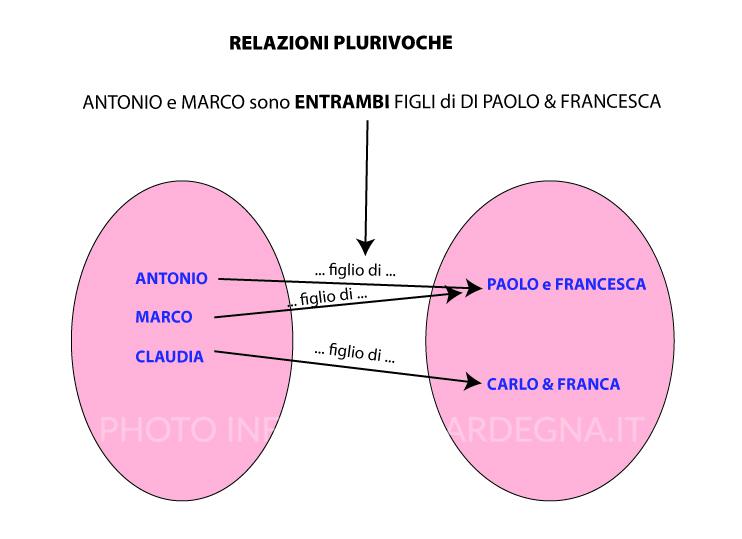
- corrispondenza plurivoca – Antonio e Luigi abitano entrambi in via Lamarmora
- corrispondenza biunivoca – Antonio vive in via Lamarmora; in via Lamarmora vive Antonio
- LEGGI ANCHE: Funzioni e loro rappresentazioni, test
CORRISPONDENZA
BIUNIVOCA
Data una relazione tra A e B esiste sempre anche l’inverso (o il reciproco) tra B e A
Le funzioni
La relazione che associa gli elementi dell’insieme A a quelli dell’insieme B (e viceversa), prende il nome di funzione (da A verso B).
LA RELAZIONE è UNA FUNZIONE
Una funzione è pertanto una relazione che determina una corrispondenza univoca o biunivoca da un elemento di un insieme A ad un elemento di un insieme B e viceversa.
Non è una funzione una corrispondenza plurivoca, perché una funzione è una relazione che un elemento di un insieme stabilisce solo ed unicamente con un elemento specifico di un altro insieme.

Descrizione di una funzione
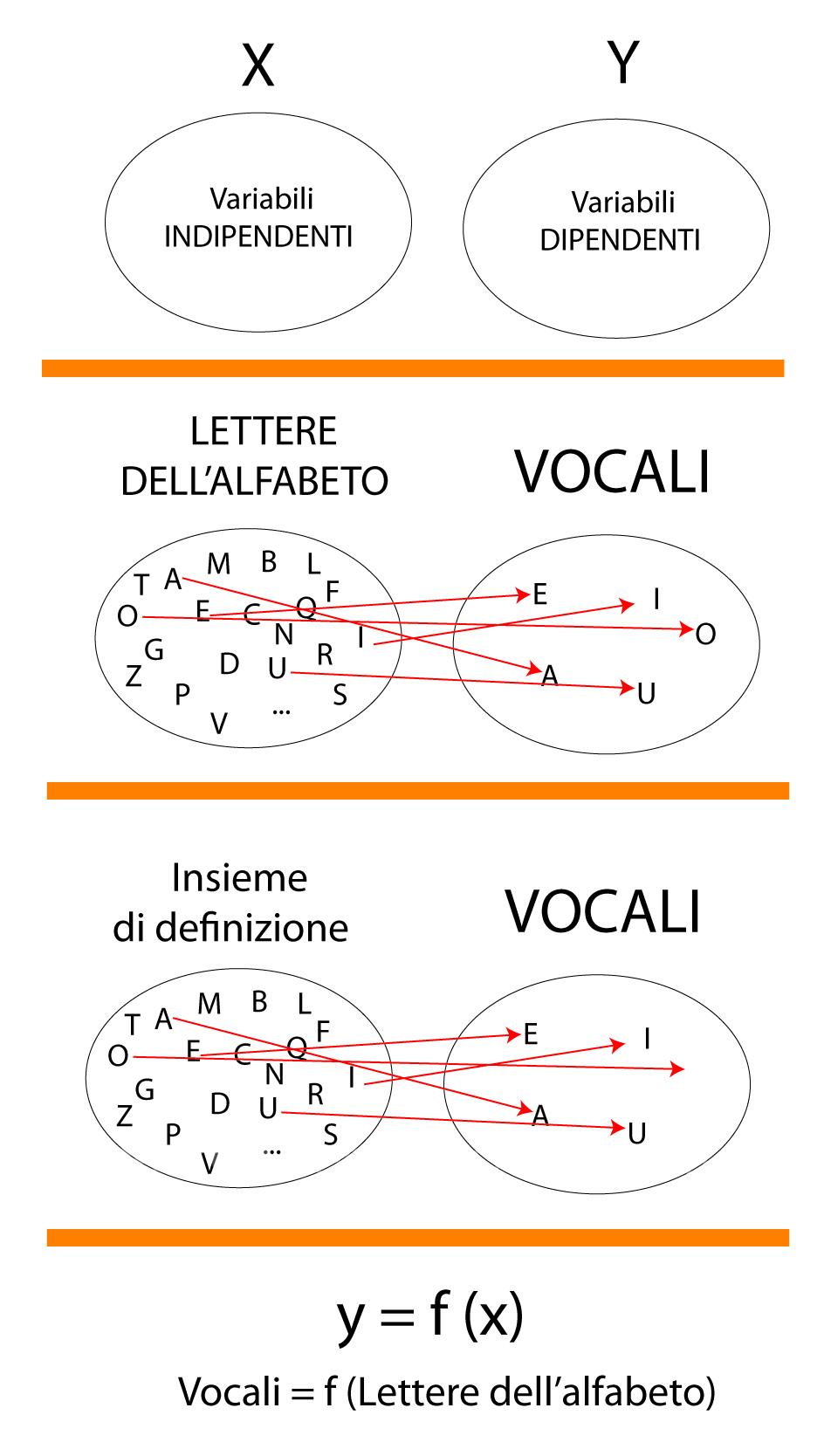
Data una funzione da A verso B, gli elementi del primo insieme, la cui scelta può essere arbitraria, sono detti variabili indipendenti e vengono indicati genericamente con la lettera x; gli elementi del secondo insieme, che sono in corrispondenza con quelli del primo, si dicono variabili dipendenti e si indicano genericamente con la lettera y.
Per esprimere che x è variabile nell’insieme A si usa la notazione x € A (leggi x appartiene ad A, o x è variabile in A.
Inoltre per indicare che esiste una funzione che lega y ad x si scrive: y = f (x) (leggi: “y è funzione di x” o, semplicemente, “y è uguale a f di x”). , dove f è l’iniziale della parola funzione.
L’insieme A in cui varia x viene detto insieme di definizione della funzione; l’elemento y, viene detto valore che la funzione assume in x.