La Proiezione di Mercatore è una rappresentazione cartografica cilindrica conforme ideata nel 1569 dal cartografo fiammingo Gerardus Mercator, utilizzata soprattutto per la navigazione marittima e aerea. Questa proiezione conserva gli angoli e le forme locali, rendendola ideale per tracciare rotte a direzione costante: sulla carta di Mercatore le rotte lossodromiche (a prua costante) appaiono come linee rette, semplificando l’uso della bussola e la pianificazione della navigazione. Tuttavia, la proiezione di Mercatore presenta una forte deformazione delle superfici alle alte latitudini, ingrandendo progressivamente le aree verso i poli. Ancora oggi è ampiamente utilizzata nelle carte nautiche, nei sistemi di navigazione e nelle mappe digitali, grazie alla sua precisione angolare e alla facilità di utilizzo per il calcolo delle rotte.
- Guarda anche: Dalla Carta Geografica alla Carta Nautica
Dal 3D al 2D: le proiezioni cartografiche e la navigazione
Per rendere la navigazione più precisa e sicura, è stato necessario trasformare la superficie tridimensionale della Terra in una rappresentazione bidimensionale. Il nostro pianeta ha infatti una forma sferica (più precisamente un geoide) e non può essere riportato su un piano senza utilizzare specifici metodi matematici.
Le proiezioni cartografiche nascono proprio con questo obiettivo: trasferire la superficie terrestre su una carta piana in modo chiaro, leggibile e funzionale. Grazie a queste tecniche è possibile rappresentare mari, coste, porti e punti di riferimento, rendendo le mappe strumenti essenziali per la navigazione.
La trasformazione dal 3D al 2D ha permesso di tracciare rotte, misurare distanze, determinare coordinate geografiche e pianificare viaggi con maggiore precisione e affidabilità. Questo processo ha posto le basi della cartografia moderna e dello sviluppo delle carte nautiche, ancora oggi fondamentali per la navigazione marittima e aerea.
La nascita della carta nautica nei Paesi Bassi
Il contributo di Gemma Frisius
Un ruolo importante nello sviluppo della cartografia moderna e delle carte nautiche fu svolto dal matematico e cosmografo fiammingo Gemma Frisius (1508–1555). Studioso di matematica, astronomia e geografia, Frisius applicò metodi scientifici innovativi alla rappresentazione della Terra e all’orientamento geografico. Insegnò all’università e contribuì alla diffusione di nuove tecniche di misurazione e costruzione delle mappe, fondamentali per la navigazione.
Mercatore e la carta nautica moderna
Tra i suoi allievi figurava il geografo e cartografo fiammingo Gerardus Mercator (1512–1594), nato Gerard Kremer. Mercatore si dedicò allo studio della matematica, dell’astronomia e della geografia, sviluppando un modello cartografico destinato a rivoluzionare la navigazione.
Nel 1569 realizzò la celebre Proiezione di Mercatore, una rappresentazione della Terra che consente di tracciare rotte a direzione costante come linee rette sulla carta. Questo sistema è alla base della moderna carta nautica e rimane ancora oggi uno degli strumenti fondamentali per la pianificazione delle rotte e la navigazione.
La distorsione delle superfici nella Proiezione di Mercatore
Il mappamondo è una rappresentazione 3D (SFERA) della Terra, la carta geografica di Mercatore è una rappresentazione 2D (PIANO) della Terra.
Non si può passare dalla 3D alla 2D senza distorsioni, perché “aprendo” la sfera geometricamente c’è sempre un parametro che subisce una distorsione (o la forma, o le aree, o le distanze).
La proiezione di Mercatore ha le seguenti caratteristiche:
- Cilindrica – Perché abbiamo proiettato i punti su un cilindro
- Centro-grafica – Perché i punti sono partiti dal centro della terra
- Conforme – Perché mantiene le forme dei paesi
Quindi, le forme dei paesi sono vere. Infatti, le rotte navali sono esatte. Quello che è distorto sono le aree dei paesi, ovvero la superficie: più ci spostiamo verso i poli le distanze aumentano e i paesi sono rappresentati sempre più grandi
La distorsione di un’immagine proiettata
Il problema della distorsione di Mercatore è esemplificata dal concetto di immagine distorta quando la si proietta su una parete. Se io proietto un’immagine sulla parete, l’immagine proiettata risulterà più grande della realtà. E più lontano sposto questa proiezione, più grande è l’immagine.
Ma se voglio rispettare il parametro della mia altezza, devo proiettare anche un metro posto vicino a me e in proiezione il centimetro continuerà ad aumentare: in questo modo la figura proiettata è diversa dalla realtà, ma rispetta le misure.
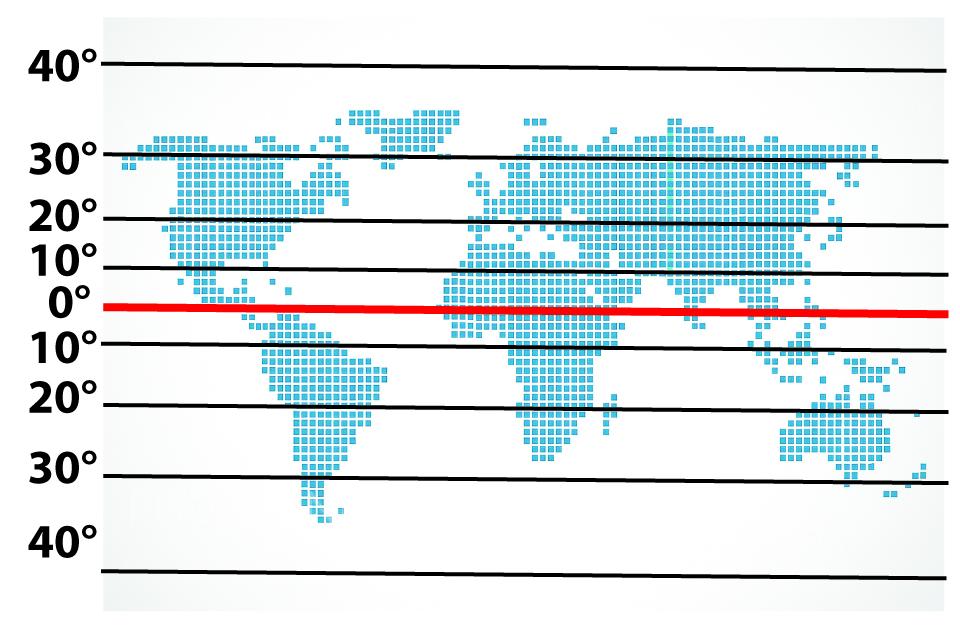
Se osserviamo la proiezione di Mercatore notiamo che man mano che ci allontaniamo dall’equatore la distanza tra i paralleli aumenta. Non hanno cioè una distanza costante come invece avviene per i meridiani.
Proiezione eurocentrica
La distorsione di Mercatore
La proiezione di Mercatore:
mantiene angoli e direzioni corrette (utile ai naviganti),
ma distorce enormemente le superfici, ingrandendo tutto ciò che è lontano dall’equatore.
La distorsione aumenta con la latitudine
Il fattore di scala aumenta con la latitudine. Questo significa che:
all’equatore: scala = 1 → nessuna distorsione
a 45°N (latitudine di gran parte dell’Europa): scala ≈ 1,41 → tutto è gonfiato del 41%
a 60°N: scala = 2 → raddoppio della dimensione
a 80°N: scala ≈ 5,76 → esplosione della superficie (come la Groenlandia che sembra enorme)
➡️ La distorsione aumenta perché sali di latitudine, non perché sei in alto o in basso sulla carta.
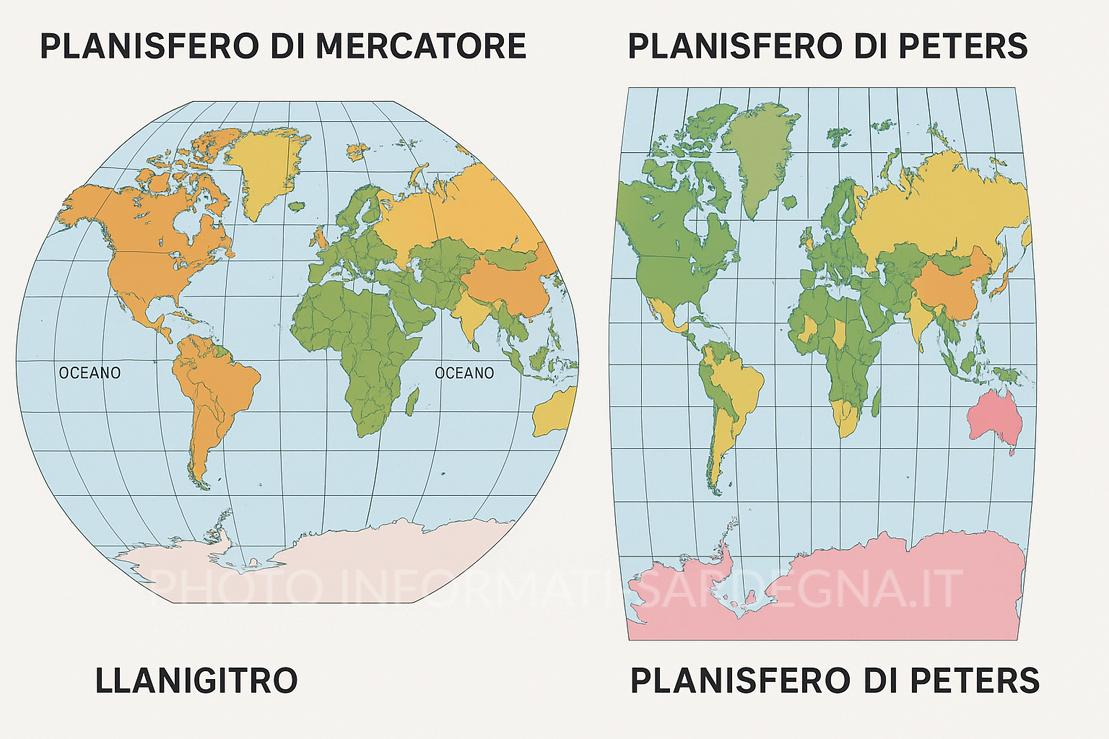
Il planisfero di Peters
Mercatore mette l’equatore al centro, ma l’emisfero nord appare molto più grande del sud perché la proiezione dilata le superfici alle alte latitudini.
Peters non dilata le superfici e mostra le dimensioni reali dei continenti, ma storce le forme.
Mercatore continua a essere usata perché è conforme, cioè mantiene angoli e forme locali corretti → indispensabile in navigazione.
🔹 1. La Terra è una sfera (approssimativamente)
Sulla superficie sferica reale, i meridiani (le linee verticali che vanno da polo a polo) si incontrano ai poli e quindi non sono paralleli tra loro.
La distanza reale tra due meridiani diminuisce man mano che ci si allontana dall’Equatore verso i poli.
🔹 2. La proiezione di Mercatore
La proiezione di Mercatore è un tipo di mappa cilindrica.
Immagina di “avvolgere” un cilindro intorno alla Terra, toccandola all’equatore, e poi di proiettare i punti della superficie terrestre su quel cilindro.
- Paralleli: le linee orizzontali
- Meridiani: le linee verticali
Quando si “srotola” il cilindro, otteniamo una carta rettangolare:
I paralleli vengono disegnati come linee orizzontali parallele e equidistanti.
I meridiani diventano linee verticali parallele (e non più convergenti come sulla sfera).
🔹 3. Cosa succede
Per poter disegnare i meridiani verticali e paralleli, la proiezione deforma le distanze:
Vicino all’equatore, la deformazione è minima.
Verso i poli, la scala aumenta enormemente → i meridiani appaiono più distanti tra loro.
Per questo le regioni polari sembrano molto più grandi (esempio: la Groenlandia sembra grande quasi come l’Africa, ma in realtà è circa 14 volte più piccola!).
La scala della carta nautica aumenta
man mano che ci si avvicina ai poli
Nella proiezione di Mercatore le regioni polari sembrano più grandi rispetto all’equatore perché la scala della mappa aumenta progressivamente con la latitudine,
facendo apparire dilatate le aree vicine ai poli.
Nella proiezione di Mercatore la scala non è la stessa ovunque:
all’equatore è “normale”,
man mano che ti sposti verso i poli, la scala aumenta sempre di più.
In pratica:
un tratto di 100 km alla latitudine dell’equatore potrebbe occupare, ad esempio, 1 cm sulla mappa;
alla latitudine della Scandinavia, gli stessi 100 km potrebbero occupare 2 o 3 cm;
vicino ai poli la scala tende addirittura all’infinito.
Quindi:
- all’Equatore 1 km = 1 cm sulla carta → Scala base: 1 : 100.000.
100 km = 1 cm sulla mappa
100 km = tra 2 e 3 cm in Scandinavia
La scala aumenta con la latitudine
🔹 ✅ In sintesi
I meridiani si “allontanano” nella proiezione di Mercatore non perché sulla Terra lo siano, ma perché la proiezione tenta di trasformare una superficie sferica in un piano rettangolare mantenendo gli angoli corretti (ma distorcendo le distanze).
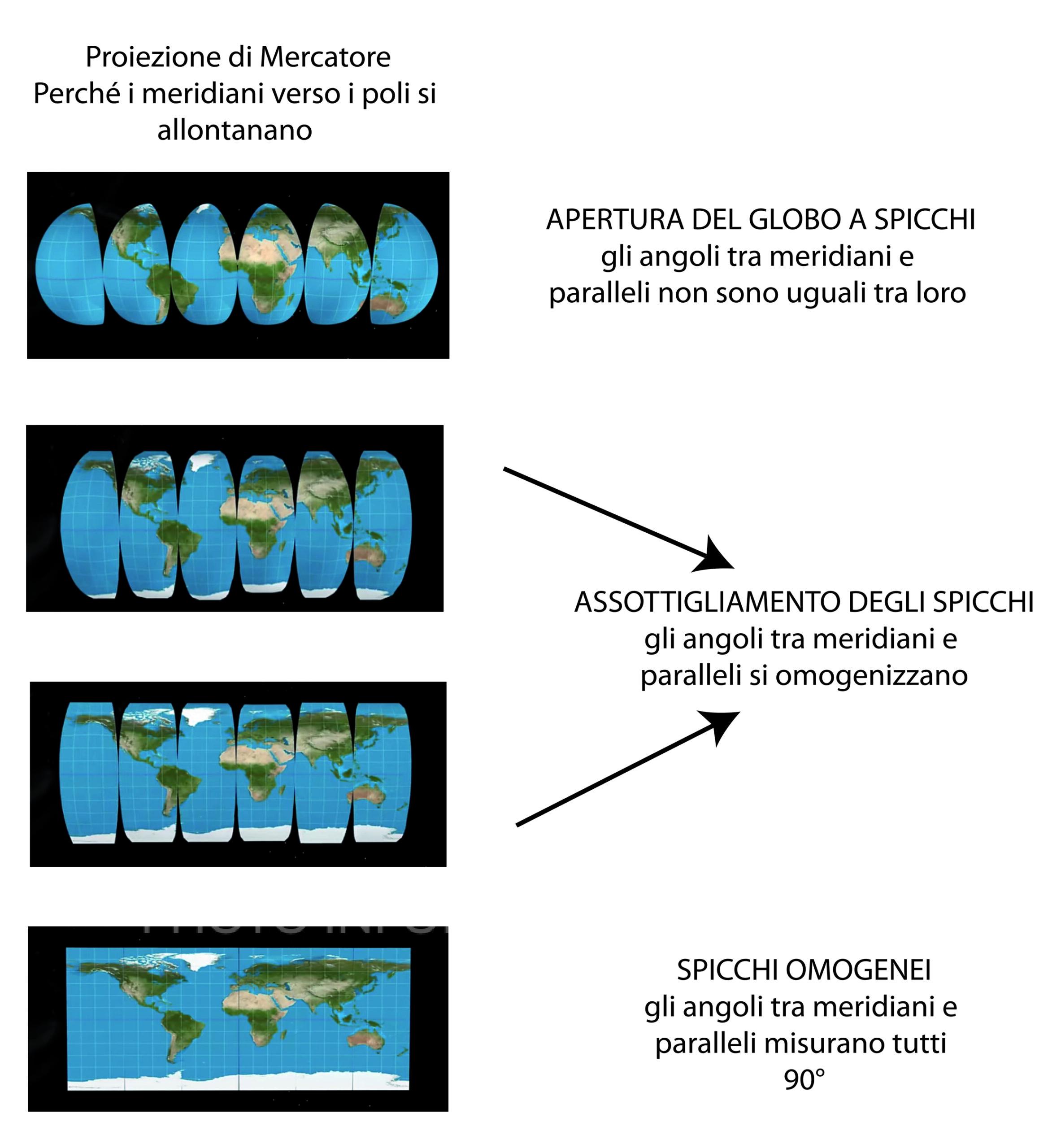
Ecco un’analisi punto per punto:
🔹 1. “Apertura del globo a spicchi”
Corretto:
La Terra (sfera) viene idealmente “tagliata” in spicchi delimitati dai meridiani.
In questa fase, gli angoli tra meridiani e paralleli non sono uguali, perché sulla sfera convergono ai poli.
🔹 2. “Assottigliamento degli spicchi”
Corretto:
Per ottenere una rappresentazione su un piano, gli spicchi vengono assottigliati per rendere più regolari gli angoli tra meridiani e paralleli.
L’obiettivo della proiezione di Mercatore è preservare gli angoli (proiezione conforme).
Si inizia a “distendere” le aree vicino ai poli per mantenere gli angoli a 90°.
🔹 3. “Spicchi omogenei – gli angoli tra meridiani e paralleli misurano tutti 90°”
Corretto anche questo:
Nella proiezione finale, i meridiani diventano linee verticali parallele, i paralleli linee orizzontali parallele.
Gli angoli tra loro sono tutti 90°, ma ciò comporta un’enorme dilatazione delle aree verso i poli (da cui la deformazione classica della proiezione di Mercatore).
⚠️ Nota interpretativa
La grafica non rappresenta un processo “fisico” realmente eseguito, ma una metafora visiva utile per capire l’effetto geometrico.
In realtà, la proiezione di Mercatore deriva da una trasformazione matematica (logaritmica) che “espande” le latitudini man mano che ci si avvicina ai poli.
✅ In sintesi
| Aspetto | Valutazione |
|---|---|
| Idea generale | ✅ Corretta |
| Spiegazione degli angoli | ✅ Corretta |
| Rappresentazione visiva | ✅ Didatticamente efficace |
| Precisione geometrico-matematica | ⚠️ Semplificata, ma accettabile per scopi divulgativi |
| Proprietà | Effetto nella proiezione di Mercatore |
|---|---|
| Angoli locali | ✅ Conservati (proiezione conforme) |
| Aree | ❌ Deformate (enorme espansione ai poli) |
| Distanze tra meridiani | 🔼 Aumentano verso i poli |
| Poli | 🚫 Non rappresentabili (y → ∞) |
L’isogonia della carta nautica
L’isongonia di una carta nautica consiste nella proprietà di una carta nautica di mantenere gli angoli della realtà. Ovvero, l’angolo di rotta disegnato sulla carta nautica è la stessa per quella rotta nella realtà.
L’isogonia di una carta nautica è una proprietà fondamentale della proiezione di Mercatore.
✔ Significato semplice
Una carta è isogona quando mantiene invariati gli angoli:
le direzioni sulla carta corrispondono alle direzioni reali sulla Terra.
In altre parole:
👉 Gli angoli misurati sulla carta sono uguali agli angoli reali tra le direzioni sul globo.
✔ Cosa comporta questo nella pratica nautica?
Sulla carta di Mercatore:
i meridiani e i paralleli si incontrano sempre con angolo di 90°;
una rotta a prua costante (rotta lossodromica) appare come una linea retta.
Quindi un navigatore può:
tracciare una rotta costante tirando una retta sulla carta,
misurare l’angolo rispetto al nord vero con un goniometro (o il compasso parallelo),
e seguire quella rotta in mare.
👉 Per questo Mercatore è utilissima nella navigazione.
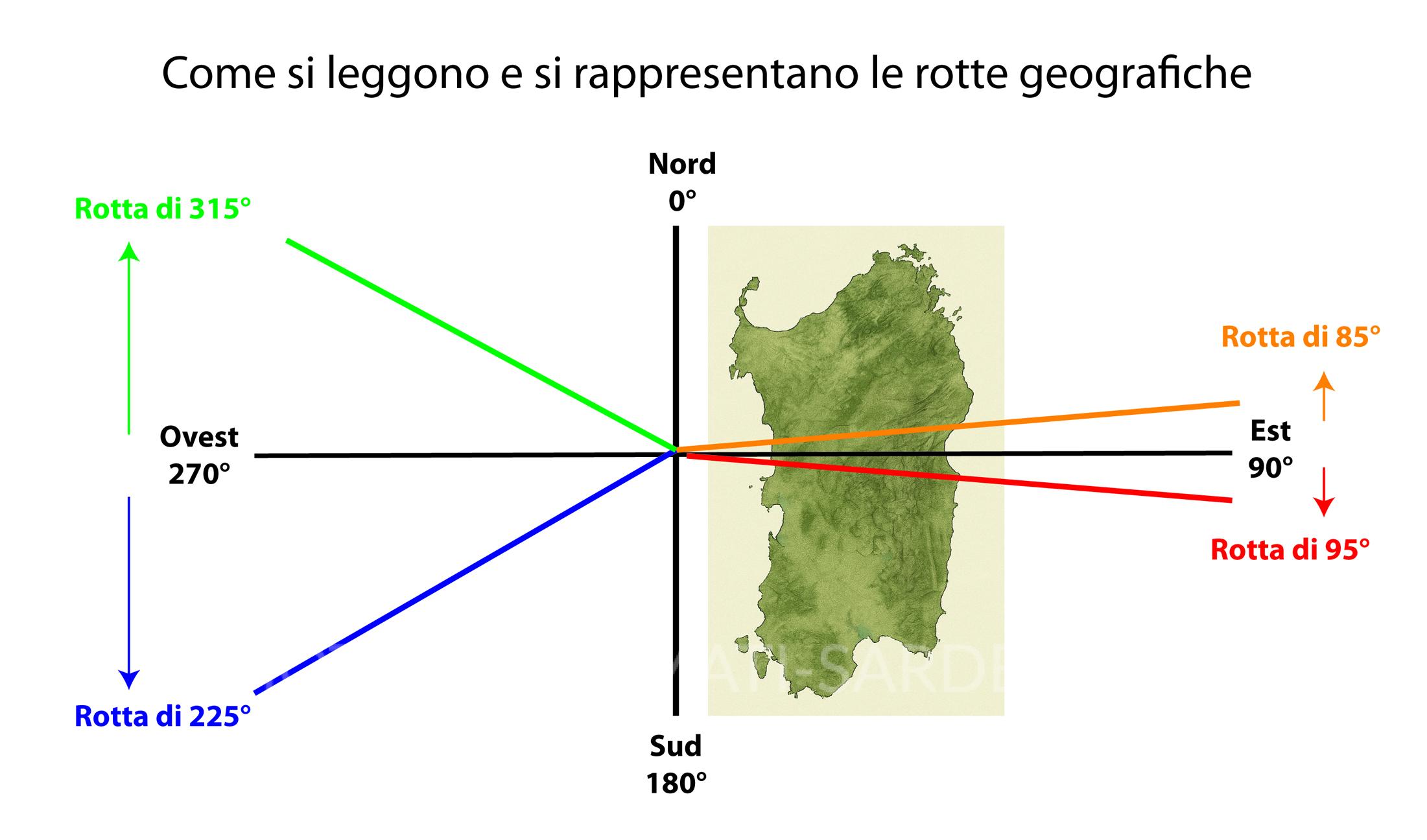
“rotta nautica o aerea” = “direzione di navigazione
la direzione che un’imbarcazione (o un aereo) segue o deve seguire rispetto al Nord geografico o magnetico.
Quindi, la rotta indica l’angolo di prua (espresso in gradi da 0° a 360°) che la direzione del moto forma con il Nord.
Su una carta di Mercatore, seguire la “linea retta” significa seguire una rotta a prora costante.
Esempi
| Rotta | Direzione corrispondente |
|---|---|
| 0° o 360° | Nord |
| 90° | Est |
| 180° | Sud |
| 270° | Ovest |
| 45° | Nord-Est |
| 225° | Sud-Ovest |
👉 Quindi, se la nave ha una rotta 95°, significa che naviga verso Est con una piccola deviazione verso Sud.
In altre parole: direzione 95° rispetto al Nord.
3. Attenzione: “rotta” ≠ “traiettoria”
La rotta è la direzione prevista o teorica da seguire.
La traiettoria reale (cioè la linea che la nave percorre effettivamente) può differire per effetto di:
correnti marine,
vento,
deriva,
errori di governo.
👉 Per questo si parla anche di:
rotta vera (rispetto al Nord geografico),
rotta magnetica (rispetto al Nord magnetico),
rotta effettiva o rotta reale (quella realmente seguita sull’acqua).
ROTTA REALE = è la direzione (angolo) – Indica sempre qualcosa riferito al Nord vero (il Nord geografico)
ROTTA VERA = è la traiettoria (percorso) – Indica qualcosa che è realmente accaduto, effettivamente percorso, di fatto avvenuto
Rotta: 👉 È un angolo. Indica la direzione del moto.
Traiettoria: 👉 È una linea. Indica il percorso disegnato.
La traiettoria è il risultato fisico della navigazione.
La rotta effettiva è l’angolo che descrive la direzione istante per istante di quella traiettoria.
✔ Esempio pratico
Rotta impostata: 090°
C’è corrente verso nord → la nave viene spinta verso l’alto.
La nave avanza, ma la scia non è perfettamente a 090°.
In questo caso:
La rotta effettiva è, ad esempio, 082°
La traiettoria è la linea curva o deviata rispetto alla rotta teorica.
✅ In sintesi
🔹 “Rotta nautica” = direzione di navigazione, espressa in gradi a partire dal Nord.
È il “verso” in cui ci si muove sul mare, non necessariamente la linea realmente percorsa, ma quella teorica o pianificata.
In cartografia nautica o geografica, le rotte si esprimono sempre come angoli misurati dal Nord in senso orario da 0° a 360°:
| Direzione | Gradi |
|---|---|
| Nord | 0° o 360° |
| Est | 90° |
| Sud | 180° |
| Ovest | 270° |
Rotta = percorso pianificato, teorico, direzione da seguire.
Traiettoria = percorso reale realmente seguito.
✔ In aviazione
La rotta è il percorso orizzontale previsto (Route).
La traiettoria include anche l’andamento verticale (salita, crociera, discesa).
Ecco un’analisi punto per punto:
🔹 1. “Apertura del globo a spicchi”
Corretto:
La Terra (sfera) viene idealmente “tagliata” in spicchi delimitati dai meridiani.
In questa fase, gli angoli tra meridiani e paralleli non sono uguali, perché sulla sfera convergono ai poli.
🔹 2. “Assottigliamento degli spicchi”
Corretto:
Per ottenere una rappresentazione su un piano, gli spicchi vengono assottigliati per rendere più regolari gli angoli tra meridiani e paralleli.
L’obiettivo della proiezione di Mercatore è preservare gli angoli (proiezione conforme).
Si inizia a “distendere” le aree vicino ai poli per mantenere gli angoli a 90°.
🔹 3. “Spicchi omogenei – gli angoli tra meridiani e paralleli misurano tutti 90°”
Corretto anche questo:
Nella proiezione finale, i meridiani diventano linee verticali parallele, i paralleli linee orizzontali parallele.
Gli angoli tra loro sono tutti 90°, ma ciò comporta un’enorme dilatazione delle aree verso i poli (da cui la deformazione classica della proiezione di Mercatore).
⚠️ Nota interpretativa
La grafica non rappresenta un processo “fisico” realmente eseguito, ma una metafora visiva utile per capire l’effetto geometrico.
In realtà, la proiezione di Mercatore deriva da una trasformazione matematica (logaritmica) che “espande” le latitudini man mano che ci si avvicina ai poli.
✅ In sintesi
Descrizione di una carta nautica
Ogni carta nautica ha una sua numerazione che troviamo in basso a destra e in alto a sinistra della carta stessa.
Se volessi navigare lungo la costa orientale della Sardegna, da Capo Monte Santo a Capo Carbonara, avrei bisogno della carta nautica n. 44 – “Da Capo di Monte Santu a Capo Carbonara” (Scala 1:100 000).
Le carte nautiche sono classificate secondo il criterio della scala.
Che cosa è la scala su una carta nautica
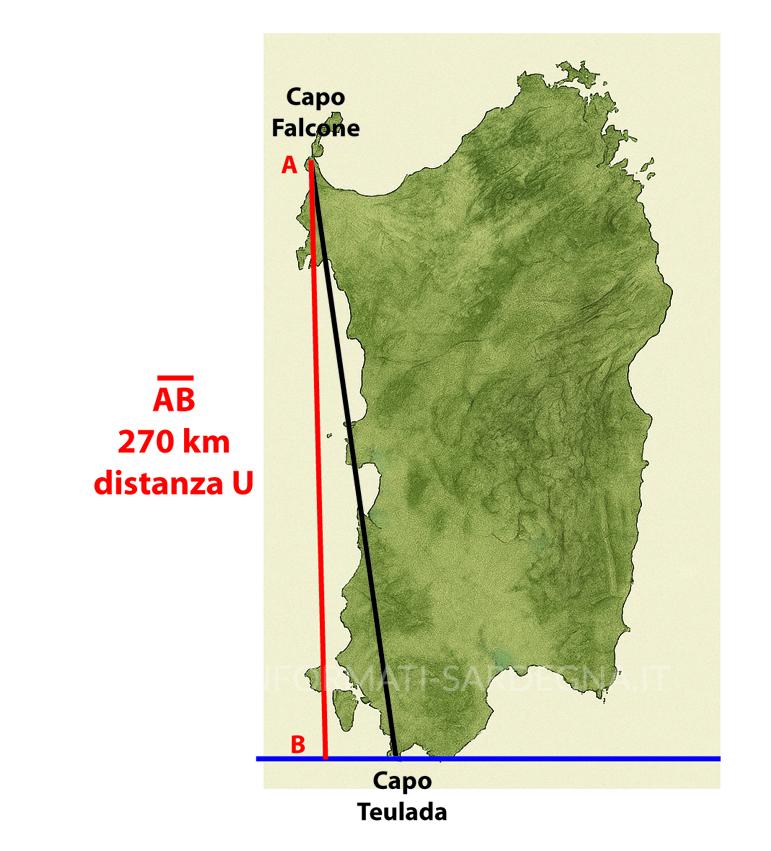
La distanza di circa 270 km per la Sardegna si riferisce alla misura in linea retta nord-sud, quindi corrisponde alla linea blu dello schema — non a quella nera diagonale.
Ecco la spiegazione dettagliata 👇
⚫️ Linea nera → distanza “obliqua” o diagonale
Rappresenta un percorso non perfettamente lungo il meridiano, quindi leggermente più lungo.
Se misurata lungo questa direzione o seguendo la costa occidentale, la distanza aumenta (≈ 290–310 km, a seconda della rotta esatta).
È utile solo se si considera una rotta reale di navigazione o un profilo costiero.
🔴 Linea rossa → distanza “geodetica verticale” di riferimento
È un riferimento teorico, che evidenzia la componente puramente nord-sud (latitudine), indipendente dalla posizione longitudinale.
✅ In sintesi
| Colore | Tipo di misura | Significato | Lunghezza stimata |
|---|---|---|---|
| ⚫️ Nera | Diagonale costiera | Rotta o linea obliqua | ≈ 290–310 km |
| 🔴 Rossa | Riferimento verticale | Differenza di latitudine pura | ≈ 270 km (identica alla blu) |
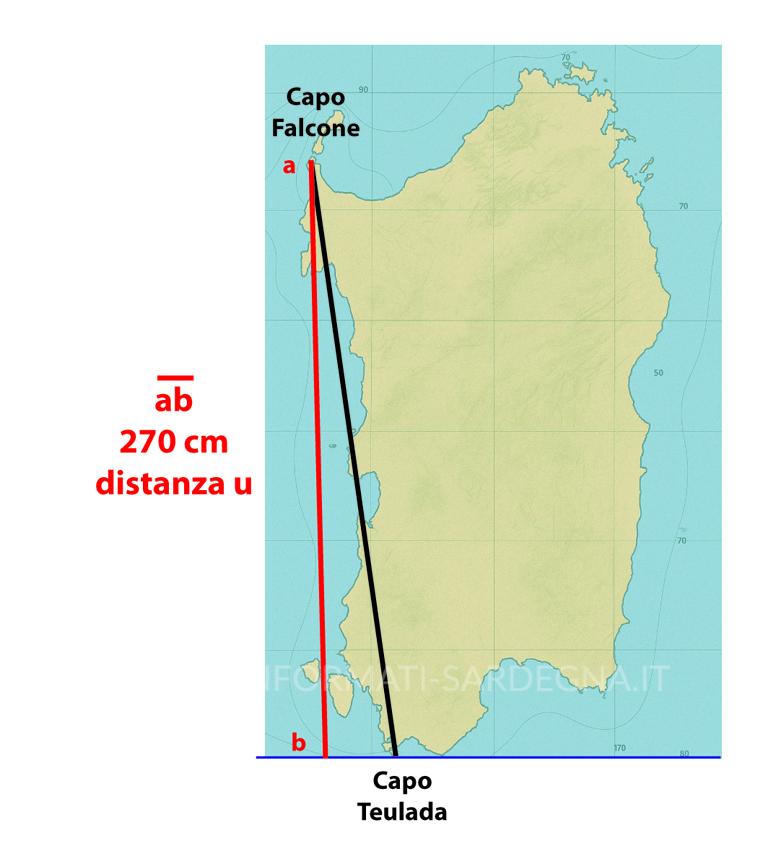
Conversione in scala di una carta nautica
Portiamo tutti i valori su una stessa grandezza. Ad esempio portiamo i chilometri in centimetri. Ovvero:
- 270 km → 27.000.000
Quindi avremo due valori:
- U maiuscolo che rappresentano la distanza reale
- u minuscolo che rapprentano la distanza in scala rappresentata nella carta nautica
Sapendo che la scala nautica è definita come un rapporto tra il segmento unitario “u/U” della carta , possiamo dire che abbiamo determinato una scala di uno a centomila (1/100.000)
Scala grande e scala piccola
1️⃣ Cos’è la scala di una carta nautica
La scala indica il rapporto tra una distanza reale sul terreno (o sul mare) e la distanza corrispondente sulla carta:
Scala=distanza sulla cartadistanza reale\text{Scala} = \frac{\text{distanza sulla carta}}{\text{distanza reale}}
Esempio:
Scala 1 : 10 000 → 1 cm sulla carta = 10 000 cm (= 100 m) reali
Scala 1 : 1 000 000 → 1 cm sulla carta = 1 000 000 cm (= 10 km) reali
⚖️ 2️⃣ Scala grande vs scala piccola
Qui sta il punto chiave:
| Tipo di scala | Esempio | Cosa significa | Uso |
|---|---|---|---|
| Scala grande | 1 : 10 000 → 1 : 50 000 | La carta mostra una piccola area ma con molto dettaglio | Porti, baie, approdi |
| Scala piccola | 1 : 500 000 → 1 : 1 000 000 | La carta mostra una grande area ma con meno dettaglio | Navigazione d’altura, pianificazione generale |
➡️ Quindi:
Più grande è il denominatore, più piccola è la scala (meno dettagliata).
📚 3️⃣ Esempi concreti di carte nautiche
| Tipo di carta | Scala tipica | Uso nautico |
|---|---|---|
| Carta d’altura | 1 : 1 000 000 | Rotte oceaniche o tra grandi isole |
| Carta di percorso o di navigazione costiera | 1 : 250 000 – 1 : 100 000 | Navigazione tra porti principali |
| Carta costiera o di approccio | 1 : 50 000 – 1 : 25 000 | Navigazione lungo costa e ingressi portuali |
| Piano nautico (portolano) | 1 : 10 000 – 1 : 5 000 | Dettaglio di porti, ancoraggi, boe, fondali |
4️⃣ In breve
| Espressione | Significato pratico |
|---|---|
| Scala grande → 1 : 10 000 | Piccola area, molto dettaglio |
| Scala piccola → 1 : 1 000 000 | Grande area, poco dettaglio |
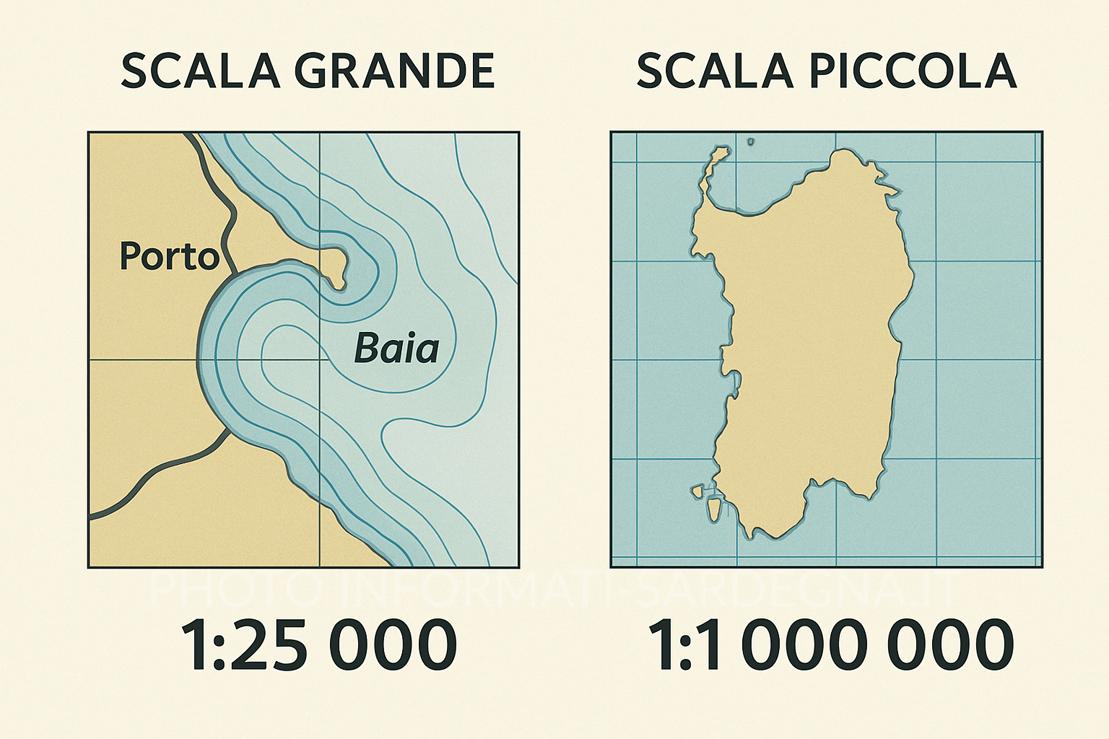
📸 Ecco l’analogia:
| Tipo di scala | Effetto “fotografico” | Cosa succede |
|---|---|---|
| Scala grande (1:10 000, 1:25 000) | 📷 Foto da vicino | Rimpicciolisce poco, quindi si vede una zona piccola ma con molti dettagli (porti, fondali, boe, fari, curve di livello ravvicinate). |
| Scala piccola (1:500 000, 1:1 000 000) | 🛰️ Foto da lontano | Rimpicciolisce molto, quindi si vede una zona grande ma con pochi dettagli (solo contorni generali della costa, poche informazioni locali). |
⚙️ Dal punto di vista geometrico
👉 Quindi nella carta 1:25 000 “ci stai dentro” molto più da vicino: ogni centimetro rappresenta una distanza molto più piccola sul terreno.
In sintesi
| Scala | Zona rappresentata | Dettaglio | Analogia |
|---|---|---|---|
| Grande (1:10 000 – 1:50 000) | piccola | alto | 📷 zoom ravvicinato |
| Piccola (1:250 000 – 1:1 000 000) | grande | basso | 🛰️ vista da lontano |
La scala grande “fotografa da vicino” (più dettagli), mentre la scala piccola “fotografa da lontano” (meno dettagli).
⚙️ Il valore “discriminante” principale
👉 Attorno a 1 : 100 000 (1 centimetro = 1 chilometro)
È il punto di riferimento che divide in pratica le carte:
Più grande di 1 : 100 000 → scala grande (dettaglio, usi locali)
Più piccola di 1 : 100 000 → scala piccola (uso generale o d’altura)
4️⃣ In sintesi
| Scala | Esempi | Tipo | Uso |
|---|---|---|---|
| 1 : 10 000 → 1 : 75 000 | porti, baie | grande | approccio, manovra |
| 1 : 100 000 → 1 : 300 000 | coste, isole | intermedia | navigazione costiera |
| 1 : 500 000 → 1 : 1 000 000 | mari e rotte | piccola | altura, pianificazione |
👉 Il valore discriminante più usato tra “scala grande” e “scala piccola”
nelle carte nautiche è intorno a 1 : 100 000.
🌍 Tipologie di Navigazione
In base alla distanza dalla costa e al tipo di mare affrontato, la navigazione marittima si suddivide in quattro categorie principali: oceanica, d’altura, costiera e portuale.
Navigazione oceanica
È quella praticata in pieno oceano, a oltre 200 miglia nautiche dalla costa. Si svolge in assenza di riferimenti terrestri visibili e richiede grande autonomia e competenza. Si utilizzano carte d’altura (scala 1 : 1 000 000 o minore) e strumenti di navigazione astronomica, oltre a GPS e sistemi satellitari. È tipica delle grandi traversate intercontinentali o oceaniche.Navigazione d’altura
Si effettua in mare aperto, ma senza superare generalmente le 200 miglia nautiche dalla costa. I riferimenti terrestri non sono visibili per lunghi tratti, ma la posizione può essere determinata con strumenti elettronici (GPS, radar, AIS, log, bussola). Si usano carte di navigazione generale o costiere (scale comprese tra 1 : 250 000 e 1 : 500 000). È la navigazione tipica tra isole o tra grandi porti del Mediterraneo.Navigazione costiera
Si svolge in vista della costa, entro circa 20–30 miglia nautiche. Consente di utilizzare riferimenti visivi (promontori, fari, boe) insieme a radar e GPS per il controllo continuo della posizione. Si impiegano carte costiere o di approccio (scale 1 : 25 000 – 1 : 100 000). È la forma di navigazione più diffusa nel diporto e nella piccola pesca.Navigazione portuale (o di manovra)
Avviene all’interno di porti, rade o canali d’ingresso, dove è necessario il massimo dettaglio cartografico per evitare bassi fondali, moli e ostacoli. Si utilizzano piani nautici o carte a grande scala (1 : 10 000 o superiore). Gli strumenti principali sono l’osservazione diretta, l’ecoscandaglio, il radar e, spesso, l’assistenza di piloti portuali.
🧭 In sintesi
| Tipo di navigazione | Distanza dalla costa | Scala delle carte | Riferimenti / strumenti principali |
|---|---|---|---|
| Oceanica | > 200 MN | ≤ 1 : 1 000 000 | Astronomici, GPS satellitare |
| D’altura | 20 – 200 MN | 1 : 250 000 – 1 : 500 000 | GPS, radar, bussola, stimata |
| Costiera | ≤ 20 MN | 1 : 25 000 – 1 : 100 000 | Fari, rilevamenti visivi, radar |
| Portuale | In porto o rada | ≥ 1 : 10 000 | Ecoscandaglio, osservazione diretta |
🗺️ Classificazione delle Carte Nautiche in base alla scala
🔴 1. Carte generali
Scala: 1 : 3 000 000 e inferiori
Sono carte a piccola scala, quindi poco dettagliate. Servono per pianificare le navigazioni oceaniche o di lunga distanza, ma non sono adatte per la condotta diretta della navigazione, poiché non riportano informazioni precise sui dettagli costieri o sui fondali.
🔴 2. Carte di atterraggio
Scala: 1 : 1 000 000 e inferiori
Sono impiegate nella navigazione d’altura quando la costa non è ancora visibile, e vengono utilizzate per l’avvicinamento alla terraferma (“atterraggio”). Si abbandonano non appena sono disponibili carte a scala maggiore, più dettagliate.
🔴 3. Carte costiere
Scala: da 1 : 300 000 / 1 : 250 000 fino a 1 : 100 000
Sono considerate le carte nautiche standard per la navigazione costiera. Forniscono un buon compromesso tra ampiezza di copertura e livello di dettaglio, risultando ideali per la transizione tra la navigazione d’altura e quella costiera.
🔴 4. Carte dei litorali
Scala: da 1 : 100 000 a 1 : 30 000
Sono carte a scala maggiore rispetto alle carte costiere, quindi più dettagliate. Sono indispensabili per condurre la navigazione in prossimità della costa, permettendo di conoscere con precisione la morfologia dei fondali, la posizione di fari, boe e punti di riferimento utili alla navigazione.
🔴 5. Piani nautici
Scala: da 1 : 20 000 a 1 : 5 000
Rappresentano porti, rade e aree di approdo. Riportano informazioni molto dettagliate su ormeggi, segnalamenti, pericoli, fondali e infrastrutture portuali, risultando quindi fondamentali per le manovre di entrata e uscita dai porti.
📘 Sintesi generale
| Tipo di carta | Scala approssimativa | Uso principale |
|---|---|---|
| Carte generali | ≤ 1 : 3 000 000 | Pianificazione di navigazioni oceaniche |
| Carte di atterraggio | ≤ 1 : 1 000 000 | Avvicinamento alla costa dopo navigazione d’altura |
| Carte costiere | 1 : 300 000 → 1 : 100 000 | Navigazione costiera e transizione dall’altura |
| Carte dei litorali | 1 : 100 000 → 1 : 30 000 | Navigazione in prossimità della costa |
| Piani nautici | 1 : 20 000 → 1 : 5 000 | Navigazione portuale e approdi |
Punti chiave
- Carta nautica = proiezione di Mercatore
- Come sviluppare una carta nautica = permette di capire dove ci troviamo
- Reticolato terrestre = longitudine e latitudine
- Estrapolare un dato dal reticolato terrestre
- In basso a sinistra della carta nautica troviamo le coordinate di inizio della carta nautica. Ad esempio: 42°19’10″N e 9°55’00” E
- In alto a destra della carta nautica troviamo le coordinate di fine della carta nautica.
- Le coordinate si leggono sempre “Latitudine e Longitudine” (es. 42°19’10″N, 9°55’00″E). Queste misure non sono distanze, ma misure angolari.
La differenza tra distanze e misure angolari
- Misure angolari = indicano posizioni sulla sfera terrestre
- Distanze lineari = indicano spazi reali sulla superficie
🧭 1. Misure angolari = indicano posizioni sulla sfera terrestre
Le coordinate geografiche (latitudine e longitudine) non sono espresse in metri o chilometri, ma in angoli misurati rispetto al centro della Terra.
Unità di misura:
Gradi (°)
Primi (′) → 1° = 60′
Secondi (″) → 1′ = 60″
Latitudine: angolo tra l’equatore e il punto osservato.
Longitudine: angolo tra il meridiano di Greenwich e il meridiano passante per il punto.
📌 Esempio:
Una latitudine di 42° N significa che il punto si trova su un parallelo che forma un angolo di 42° con l’Equatore.
👉 Le misure angolari non danno direttamente una distanza, ma servono per localizzare un punto sulla superficie terrestre.
2. Distanze lineari = indicano spazi reali sulla superficie
La distanza è quanto spazio c’è realmente tra due punti.
Si misura in:
Miglia nautiche (NM) → usate in navigazione marittima e aerea
Chilometri (km) → usati sulla terraferma
Metri (m) per distanze più piccole.
✅ 1 miglio nautico = 1,852 km
📌 Esempio:
Due punti distanti 1° di latitudine l’uno dall’altro sono separati da 60 miglia nautiche, ossia circa 111 km.
✅ 1° di Latitudine = 60 NM = 111,12 Km
✅ 1° di Longitudine = 60 MN × cos(latitudine)
1° di longitudine ≠ 60 NM ≠ 111,12 km (tranne all’equatore)
La distanza tra due meridiani dipende dalla latitudine, perché i meridiani si avvicinano man mano che si va verso i poli.
📌 Esempi
Equatore (0°) → 60 NM (111 km) ✔️
30° → 60 × cos(30°) = 52 NM
45° → 60 × cos(45°) = 42 NM
60° → 60 × cos(60°) = 30 NM
Poli (90°) → 0 NM
📌 In sintesi
Latitudine: sempre 60 NM per grado
Longitudine: varia con la latitudine, solo all’equatore vale 60 NM
📐 3. Relazione tra misure angolari e distanze
Sulla Terra:
1° di latitudine = circa 60 NM
1′ (primo) = 1 NM (miglio nautico ≈ 1.852 m)
1″ (secondo) = 1/60 NM ≈ 30,9 m
Per la latitudine questa relazione è costante, perché i paralleli sono equidistanti.
Per la longitudine invece la distanza diminuisce avvicinandosi ai poli, perché i meridiani convergono:
All’Equatore: 1° di longitudine ≈ 60 NM
A 42° N (come nell’esempio): 1° di longitudine ≈ 60 × cos(42°) ≈ 44,6 NM
Ai poli: 1° di longitudine = 0 NM (i meridiani si incontrano).
📊 4. In sintesi
| Aspetto | Misura angolare | Distanza lineare |
|---|---|---|
| Unità | °, ′, ″ | NM, km, m |
| Cosa indica | Posizione sulla Terra | Spazio reale tra due punti |
| Tipo di misura | Angolo al centro della Terra | Lunghezza sulla superficie |
| Costanza tra i gradi | Sì per la latitudine, no per la longitudine | Variabile con la latitudine |
| Conversione tipica | 1′ = 1 NM | 1 NM ≈ 1.852 m |
✅ Esempio pratico
Se due fari si trovano su:
42°00’00″N, 9°00’00″E
42°01’00″N, 9°00’00″E
→ la differenza è di 1′ in latitudine → distanza ≈ 1 NM (1,852 km).
Miglio Nautico e Grado di Latitudine
Il miglio nautico è collegato al grado di latitudine perché nasce proprio dalla geometria della Terra, non da una scelta arbitraria.
Ecco la spiegazione chiara:
🌍 1. La latitudine misura la distanza dal polo sud al polo nord
La latitudine va da:
0° all’equatore
+90° al Polo Nord
–90° al Polo Sud
Ogni grado di latitudine rappresenta una distanza reale sulla superficie terrestre.
E questa distanza è quasi identica ovunque:
👉 1° di latitudine ≈ 111,12 km = 60 NM
🧭 2. Ogni grado è diviso in 60 minuti (′)
Come un’ora:
1° = 60′
1′ è quindi una piccolissima parte del meridiano terrestre.
📏 3. Un minuto di latitudine ha una distanza fisica costante
Se 1° ≈ 111,12 km, allora:
111,12/60 = 1,852 km = 1 miglio nautico
- 1° di latitudine = 111,12 km;
- 1 miglio nautico = 1,852 km;
- 1,852 km x 60 = 1° di latitudine
- 111,12/1,852 km = 60 miglia
Distanza in chilometri di latitudine tra Poli ed Equatore:
1° di latitudine ≈ 111,12 km
Tra Equatore e Polo ci sono 90°
Quindi:
- 111,12×90=9 999 km (circa)≈10 008 km
🚢 4. Perché questa scelta è utilissima in navigazione?
Perché sulla carta geografica (specialmente sulle carte nautiche):
Sposti il compasso verticalmente sulla scala delle latitudini → misuri la distanza in miglia nautiche
Non servono conversioni
La Terra ha una forma che rende il minuto di latitudine quasi costante ovunque
È un sistema naturale, facile, logico e universale.
🎯 In sintesi
✔ Il miglio nautico è stato definito come la distanza corrispondente a 1’ di latitudine.
✔ Questa distanza è quasi identica in ogni punto della Terra.
✔ Per questo 1 NM = 1,852 km.
✔ Ecco perché il miglio nautico è legato alla latitudine, e non alla longitudine (che varia con la latitudine).
Come determinare le distanze su una carta nautica
La misurazione di una altezza, ovvero di una distanza è variabile in base alla distanza, essendo una proiezione, pertanto la misura della distanza va presa solo sull’asse delle latitudini.
Può essere presa sull’asse delle longitudini solo se si naviga lungo l’equatore
Per calcolare le distanze nautiche solo latitudini
Man mano che dall’equatore ci si sposta verso i poli, la distanza tra i meridiani (e i relativi archi di circonferenza) diminuisce, fino ad avere che la distanza ai poli tra i meridiani corrisponde a 0 (zero).
Essendo dunque la misura della longitudine variabile, per misurare le distanze nautiche si considerano solo le misure delle latitudini (la distanza tra il punto e l’equatore). Può essere presa sull’asse delle longitudini solo se si naviga lungo l’equatore. Pertanto, per misurare le distanze marine tra un punto e l’altro della terra si considera solo la scala verticale della carta nautica, quella delle latitudini.
Miglio Nautico ≠ Miglio Terrestre
👉 1 miglio nautico = 1,852 km
È legato alla geometria della Terra, non a misure arbitrarie.
🚗 MIGLIO TERRESTRE (miglio “statuto” anglosassone)
✔ Usato nei paesi anglosassoni (USA, UK) per distanze su terra
👉 1 miglio terrestre = 1,609 km
| Tipo di miglio | Valore in km | Ambito d’uso |
|---|---|---|
| Nautico | 1,852 km | Navigazione (mare, aria) |
| Terrestre | 1,609 km | Strade e distanze a terra (USA, UK…) |
Miglio nautico e miglio terrestre
👉 Il miglio nautico è più lungo del miglio terrestre. Ecco le differenze a confronto:
- 1 Miglio Nautico = 1,852 km
- 1 miglio = 1,609 km
- 1 Miglio Nautico = 1,15 miglia terrestri
I primi e gli archi di latitudine e i gradi
- Un miglio corrisponde a un primo sulla scala delle latitudini della carta nautica e un primo sulla scala delle latitudini corrisponde a un primo delle unità di misura angolari. Pertanto:
- Sui bordi laterali della carta nautica (in proiezione di Mercatore) trovi la scala delle latitudini:
È graduata in gradi (°) e primi (′) di latitudine.
Ogni piccola divisione corrisponde quindi a un primo, ovvero un minuto d’arco di latitudine.
