Solidi, superfici, linee e punti

LA GEOMETRIA
La geometria è la scienza dello spazio: i punti, le linee, le superfici e i solidi sono i pilastri su cui essa si fonda.

STORIA DELLA GEOMETRIA
La storia della geometria si articola in tre passaggi fondamentali:

1. Sumeri, Babilonesi ed Egizi – iniziano l’uso di concetti geometrici per finalità pratiche (commercio, agricoltura);
2. Antichi Greci (Talete e Pitagora) – inquadrano la geometria nella speculazione filosofica e la trasformano in teoria scientifica;
3. Euclide – fa la prima raccolta sistematica dei concetti geometrici fino ad allora conosciuti esponendoli nell’articolazione di proposizioni introduttive (i postulati) e finali (le dimostrazioni).

La geometria nasce in Medio Oriente e in Nord Africa tra il 3000 e il 2000 a.C. tra gli antichi popoli dei Sumeri, dei Babilonesi e degli Egizi i quali si servirono per primi di rappresentazioni geometriche che utilizzarono per capire il movimento degli astri (i primi e i secondi) e per ridisegnare le proprietà terriere dopo le inondazioni del Nilo (i terzi). Questi antichi popoli concepirono la geometria come una tecnica.

Grazie ai primi scambi commerciali nel Mediterraneo orientale, la geometria venne conosciuta anche nell’Antica Grecia che slegarono lo studio della geometria dalle applicazioni pratiche e svilupparono, coi primi filosofi (Talete, fondatore della Scuola Ionica e Pitagora fondatore della Scuola Pitagorica), le prime teorie geometriche. In Grecia la geometria divenne quindi una scienza, cioè una speculazione sugli argomenti geometrici per finalità conoscitive fini a se stesse, senza che queste dovessero necessariamente avere delle applicazioni pratiche.

A realizzare la prima elaborazione organica della geometria fu Euclide (IV secolo a.C. – III secolo a.C.) che tra il 306 e il 233 a.C. compendiò nei 13 libri degli Elementi, in cui espose in maniera sistematica e logica in concetti geometrici fino ad allora conosciuti che entrarono a far parte della cosiddetta “Geometria euclidea” . Euclide partiva da poche proposizioni, dette postulati (per esempio: per due punti passa una ed una sola retta), che ammettono vere intuitivamente e da queste, senza fare più ricorso all’intuizione, deduce le dimostrazioni che sono delle proposizioni di ragionamento logico.

I CONCETTI GEOMETRICI PRIMITIVI
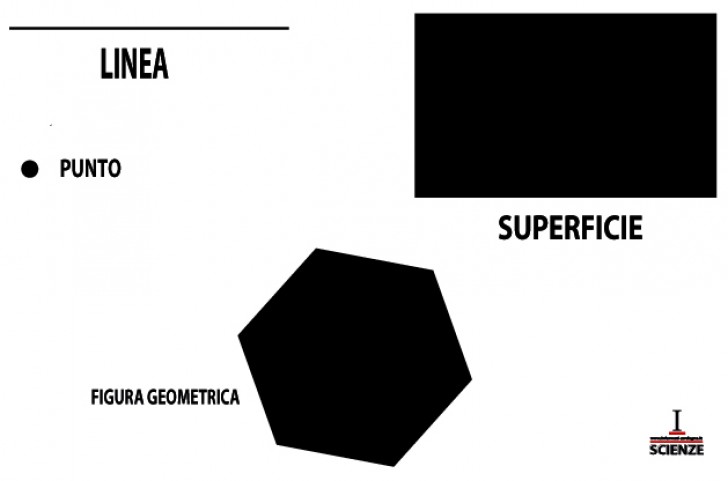
I concetti primitivi sono le rappresentazioni mentali di determinati concetti geometrici che la mente umana concepisce a priori astraendoli dalla realtà . Sono concetti primitivi:

• i corpi geometrici;
• la linea;
• il punto;
• la superficie.

CORPI MATERIALI E CORPI GEOMETRICI
Qualsiasi oggetto che ci circonda è un corpo materiale. Ogni corpo ha certe proprietà che lo distinguono dagli altri oggetti: esso ha un proprio colore, una propria forma, una propria estensione, è fatto di determinate sostanze e occupa una certa posizione nello spazio.

Quando di un corpo ci limitiamo a considerare la forma, l’estensione e la posizione, prescindendo da tutte le altre proprietà , stiamo parlando di un corpo geometrico. Un corpo geometrico si può definire anche solido geometrico.

LA FIGURA GEOMETRICA
Una figura geometrica è un insieme infinito di punti. Lo spazio è l’insieme infinito di tutti i punti.

LE SUPERFICI
Il concetto di superficie, è un concetto primitivo che rappresenta una lamina sottile senza spessore. Le superfici possono essere di quattro tipi:

• superficie piana
• superficie curva
• superficie limitata
• superficie illimitata
• superficie piana limitata
• superficie piana illimitata
• superficie curva limitata
• superficie curva illimitata

Le superficie piane illimitate vengono chiamate piani

LE LINEE
La linea è una figura geometrica formata dalla successione di posizioni di un punto in movimento. La linea geometrica è priva di spessore e di larghezza e può essere di sei tipi:

1. linea limitata – ha un’origine e una fine
2. linea illimitata – ha un’origine ma non ha una fine
3. linea chiusa – quando origine e fine coincidono sullo stesso punto
4. linea aperta – quando origine e fine non coincidono sullo stesso punto
5. linea retta – quando ha un andamento dritto
6. linea curva – quando ha un andamento curvo

IL PUNTO
Il punto è un concetto geometrico che non ha dimensioni di estensione e di forma, ma ha solo posizione. Il punto non ha parti.

LA RETTA
La retta è un tipo di linea, detta linea retta illimitata che ha un’origine ma non ha una fine.

• Per due punti distinti passa una ed una sola retta;
• I punti che appartengono ad una stessa retta si dicono allineati
• Per un punto passano un’infinità di rette, dette stella di rette.

IL PIANO
Il piano è un tipo di superficie, detta superficie piana illimitata.

• Per tre punti passa uno ed un solo piano;
• L’insieme di tre punti che appartengono ad uno stesso piano si dicono complanari;
• per una retta passano infiniti piani (stella di piani), quindi per due punti passano infiniti piani;
• Un piano qualsiasi divide lo spazio in due semispazi che si dicono opposti

POSIZIONI RECIPROCHE DI RETTE E DI PIANI

Le due entità geometriche astratte, piani e rette, possono assumere tre tipi di posizione reciproca tra loro:

1. La retta può essere giacente sul piano
2. La retta può essere parallela al piano
3. La retta può essere incidente al piano

Queste tre posizioni reciproche sono le uniche che retta e piano possono avere  

IL LINGUAGGIO DEGLI INSIEMI NELLE POSIZIONI RECIPROCHE DI PIANI E RETTE
Le posizioni reciproche di Retta e Piano possono essere riportate anche utilizzando il linguaggio degli insiemi. Ovvero:

Caso 1
Se la retta r giace sul piano α allora la retta r è inclusa nel piano alfa.

• Ovvero: r ⊂ α
• Ovvero: r ∩ α = r

Caso 2
Se la retta r è parallela al piano α allora la retta r e il piano α sono due insiemi disgiunti che danno luogo a un insieme vuoto.

• Ovvero: r ∩ α = ∅

Caso 3
Se la retta r è incidente sul piano α, allora la retta r e il piano α sono incidenti nel punto P.

Ovvero: r ∩ α = { P }

I SEMIPIANI
Quando una retta e un piano hanno due punti in comune e dunque la retta giace interamente sul piano, essa divide il piano in due semipiani in cui la retta è l’origine di questi.

POSIZIONI RECIPROCHE DI DUE RETTE. I FASCI DI RETTE
Due rette distinte r ed s possono avere in comune o un unico punto o nessuno: infatti, se avessero in comune due punti, esse coinciderebbero, dal momento che per due punti distinti passa una sola retta.

• Quando due rette hanno un punto in comune, esse sono incidenti. Ovvero: r∩ s = {p} .
• Quando due rette non hanno alcun punto in comune, esse possono essere: parallele o sghembe. Ovvero: r∩ s = {∅} .

Caso 1: rette incidenti

Quando due rette hanno un punto in comune, esse sono incidenti. Ovvero: r∩ s = {p} . In questo caso due rette incidenti individuano un piano, il piano α. 

• Caso 2/ A: rette parallele

Quando due rette non hanno punti in comune possono essere parallele

• Caso 2/ B: rette sghembe

Il Postulato delle parallele

** definizione di postulato
Un postulato è una affermazione che si ammette vera per intuizione anche senza dimostrazione.

Il Postulato delle Parallele dice che: su un punto P non appartenente ad una retta r, passa solo una retta parallela ad essa, la retta r’.