ESERCIZIO 1
Dodici cavalli mangiano 30q di biada in 25 giorni. Quanti quintali di biada saranno necessari per alimentare 18 cavalli per 15 giorni?
- Ragionamento da fare:
Se il numero di cavalli aumenta, passando da 12 a 18, la quantità di biada necessaria per sfamarli, aumenta o diminuisce? Aumenta. Rapporto di proporzionalità diretta tra numero di cavalli e quantità di biada.
Se il numero di giorni in cui viene dato il cibo, il tempo di consumo, diminuisce, passando da 25 a 15 giorni, la quantità di biada necessaria per sfamare i cavalli, aumenta o diminuisce? Aumenta. Rapporto di proporzionalità inversa tra tempo di consumo e quantità di biada.
** La biada è un nome generico per indicare qualsiasi cereale usato come foraggio. Questo termine si usa soprattutto in Toscana e nelle regioni prealpine.

ESERCIZIO 2
Per costruire un muro alto 2 metri e lungo 15 metri sono stati utilizzati 6600 mattoni. Quanti mattoni saranno necessari per costruire un muro dello stesso spessore alto 3 metri e lungo 20 metri?
- Ragionamento da fare
Se la lunghezza del secondo muro aumenta passando da 15 a 20 metri rispetto al primo, il numero di mattoni necessari da utilizzare per costruire il muro, aumenta o diminuisce? Aumenta. Rapporto di proporzionalità diretta tra lunghezza del muro e numero di mattoni necessari a costruirlo.
Se l’altezza del secondo muro rispetto al primo, aumenta passando da 2 metri a 3 metri, il numero di mattoni necessari per costruirlo aumenta o diminuisce? Aumenta. Rapporto di proporzionalità diretta tra altezza del muro e numero di mattoni necessari per costruirlo.

ESERCIZIO 3
Per costruire 120 metri di galleria 20 operai hanno lavorato per 5 giorni. Quanti giorni impiegheranno 15 operai a costruire 162 metri della stessa galleria?
- Ragionamento da fare
Se il numero di operai che vengono impiegati per costruire la seconda galleria, diminuisce passando da 20 a 15, il tempo di lavoro necessario per completare il lavoro, aumenta o diminuisce? Aumenta. Rapporto di proporzionalità inversa tra numero di operai impiegati e tempo di lavoro necessario.
Se la lunghezza della galleria aumenta, passando da 120 a 162 metri, il tempo di lavoro degli operai aumenta o diminuisce? Aumenta. Rapporto di proporzionalità inversa tra lunghezza della galleria e tempo di lavoro necessario.

ESERCIZIO 4
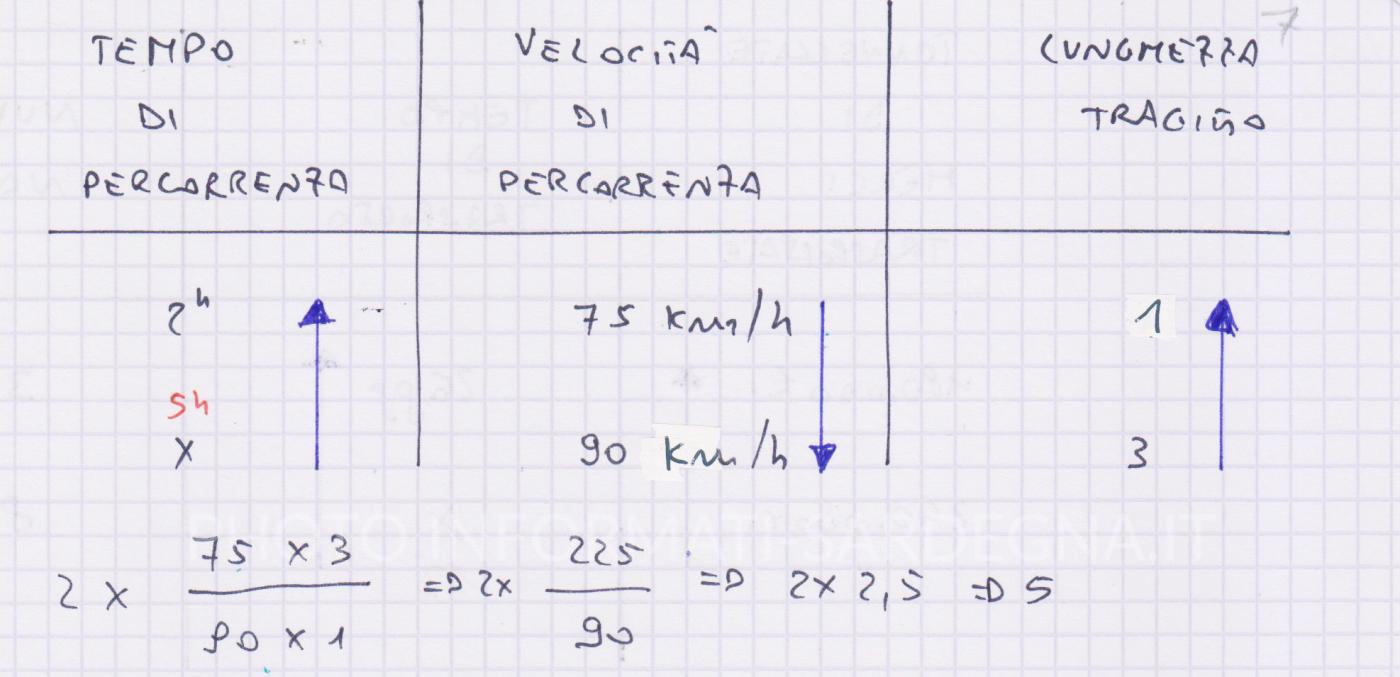
Un autocarro compie un tragitto in 2 ore viaggiando alla velocità di 75 km/h. Quanto tempo impiegherebbe a compiere un tragitto di lunghezza tripla viaggiando a 90 km/h?
- Ragionamento da fare
Se la velocità del mezzo al secondo viaggio (velocità di percorrenza) aumenta passando da 75 km/h a 90 km/h, il tempo di percorrenza per effettuare lo stesso tragitto aumenta o diminuisce? Diminuisce. Quindi il rapporto tra tempo di percorrenza e velocità di percorrenza è un rapporto di proporzionalità inversa.
Se la lunghezza del tragitto da percorrere, al secondo viaggio, aumenta triplicando rispetto al primo viaggio, il tempo di percorrenza aumenta o diminuisce? Aumenta. Quindi il rapporto tra lunghezza del tragitto e tempo di percorrenza è un rapporto di proporzionalità diretta.
ESERCIZIO 5
Una conduttura immette in un serbatoio 25 litri di acqua in 4 minuti riempendolo in 3 ore. Quanto tempo impiega a riempire il serbatoio una conduttura che immette 75 litri ogni 16 minuti?
- Ragionamento da fare
La prima operazione da fare è individuare le velocità di riempimento dei serbatoio e metterle a confronto. Il primo serbatoio viene riempito a una velocità data dal rapporto tra 25 litri e 4 minuti, ovvero: 25/4 = 6,25 L/m (si legge: 6,25 litri al minuto). Il secondo serbatoio viene riempito a una velocità data dal rapporto tra 75 litri e 16 minuti, ovvero: 75/16 = 4,68.
Da questo primo ragionamento si evince chiaramente che la prima conduttura ha una velocità di riempimento maggiore rispetto alla seconda. Quindi:
- se la velocità di riempimento del serbatoio diminuisce da 6,25 L/m a 4,25 L/m, il tempo di riempimento aumenta o diminuisce? Aumenta. Quindi il rapporto tra velocità di riempimento e tempo di riempimento è un rapporto di proporzionalità inverso.

ESERCIZIO 6
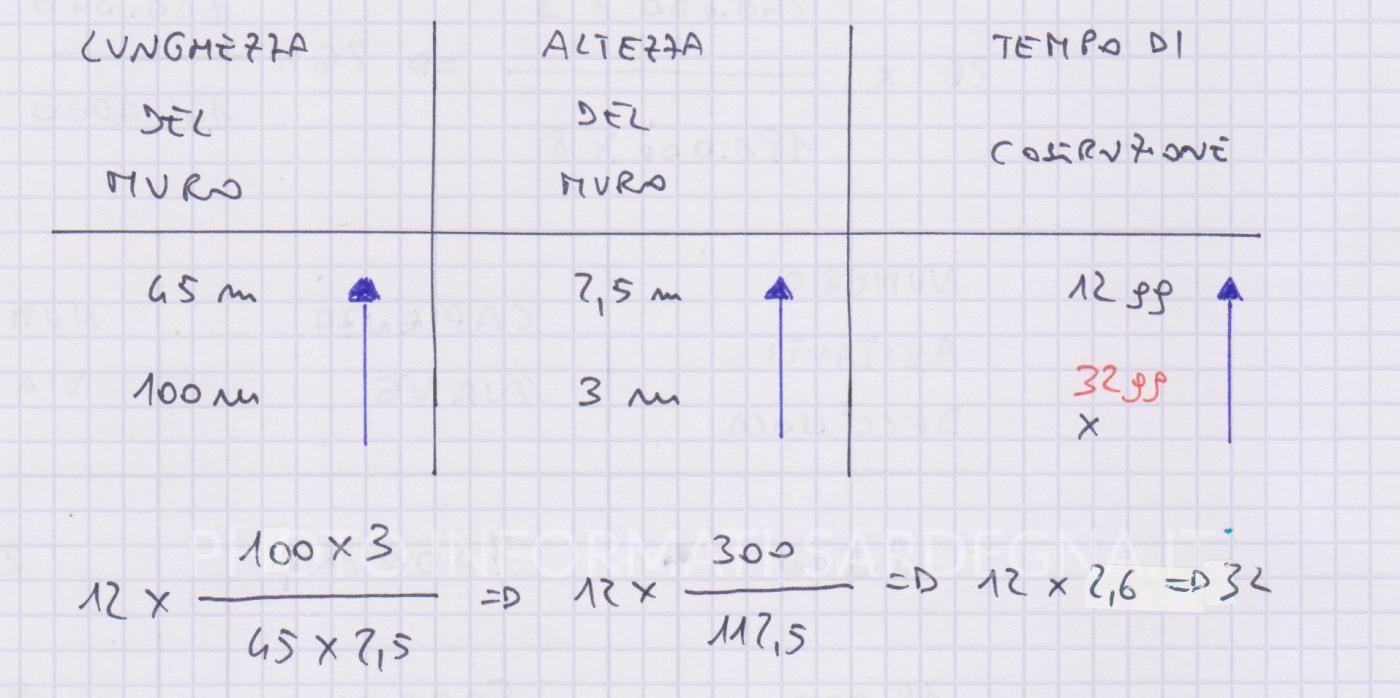
Un muro lungo 45 metri e alto 2,5 metri è stato costruito in 12 giorni. Quanti giorni saranno necessari per costruire un muro dello stesso tipo lungo 100 metri e alto 3 metri?
- Ragionamento da fare
Se l’altezza del secondo muro aumenta da 2,5 metri a 3 metri, il tempo di costruzione del secondo muro rispetto al primo, aumenta o diminuisce? Aumenta. Quindi tra altezza del muro e tempo di costruzione del muro vi è un rapporto di proporzionalità diretta.
Se la lunghezza del secondo muro aumenta passando da 45 metri a 100 metri, il tempo di costruzione del secondo muro rispetto al primo, aumenta o diminuisce? Aumenta. Quindi, tra lunghezza del muro e tempo di costruzione si stabilisce un rapporto di proporzionalità diretto.
ESERCIZIO 7
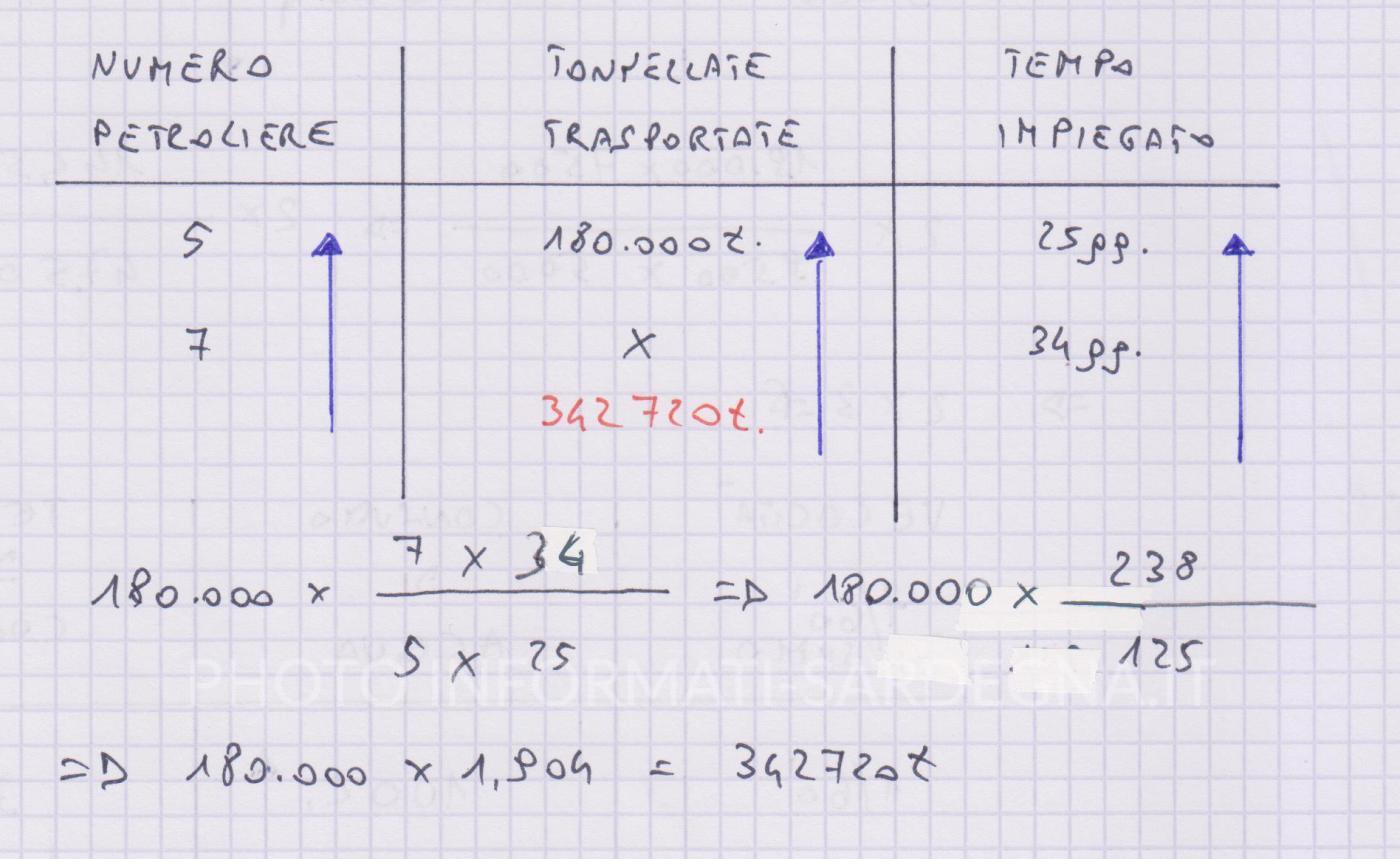
Una compagnia petrolifera trasporta con 5 petroliere 180 mila tonnellate di petrolio dal punto di imbarco alle raffinerie in 25 giorni. Che quantità di petrolio verrà trasportata da 7 navi uguali alle precedenti in 34 giorni?
- Ragionamento da fare
Se il numero di petroliere aumenta al secondo viaggio, passando da 5 a 7, rispetto al primo, le tonnellate di petrolio trasportate aumentano o diminuiscono? Aumentano. Quindi, tra numero delle petroliere e Tonnellate di petrolio trasportate si stabilisce un rapporto di proporzionalità diretto.
Se il tempo di viaggio impiegato al secondo viaggio, aumenta passando da 25 giorni a 34, la quantità di petrolio trasportate aumenta o diminuisce? Aumenta. Quindi, tra tempo impiegato e tonnellate di petrolio trasportate si stabilisce un rapporto di proporzionalità diretto.
ESERCIZIO 8
Una società trasporta 180.000 tonnellate di merci in 26 giorni con 3 navi. Quanti giorni saranno necessari per trasportare 240.000 tonnellate di merci se sono disponibili 8 navi uguali alle precedenti?
- Ragionamento da fare
Se il numero di navi al secondo viaggio aumenta passando da 3 a 8, la quantità di tempo necessario a trasportare la merce aumenta o diminuisce? Diminuisce. Quindi, tra tempo di trasporto e numero di navi, si stabilisce un rapporto di proporzionalità inverso.
Se le tonnellate di merci trasportate aumentano passando da 180 mila a 240 mila, il tempo di viaggio necessario, aumenta o diminuisce? Aumenta. Quindi, tra quantità di merce trasportata e tempo di trasporto della stessa si stabilisce un rapporto di proporzionalità diretto.

ESERCIZIO 9
Un’isola abitata da 9500 abitanti è rifornita di acqua potabile per mezzo di una nave cisterna da 7500 metri cubi, che compie 2 viaggi in un certo periodo di tempo. Quanti viaggi, nello stesso tempo, dovrà fare una cisterna da 5.000 metri cubi per rifornire un’isola con 19.000 abitanti?
- Ragionamento da fare
Se la capienza di acqua della seconda nave diminuisce passando da 7500 metri cubi a 5000 metri cubi, il numero di viaggi necessario per trasportare l’acqua nell’isola aumentano o diminuiscono? Aumentano. Quindi, tra capienza della nave e numero di viaggi si stabilisce un rapporto di proporzionalità inverso.
Se il numero di abitanti della seconda isola aumenta, passando a 19000, rispetto a quelli della prima isola, il numero di viaggi necessari per portare l’acqua potabile aumenta o diminuisce? Aumenta. Quindi tra numero di viaggi delle navi e numero di abitanti delle isole si stabilisce un rapporto di proporzionalità diretto.

ESERCIZIO 10
Uno zoo ospita per 13 giorni, 10 tra leoni e tigri e viene dato loro 210 kg di carne a testa. Quanti chilogrammi di carne servirebbero per ospitare 3 animali in più per 15 giorni anziché 10?

ESERCIZIO 11
In un hotel del golfo vengono ospitate 28 persone per 4 giorni, registrando un giro di entrate pari a 12.000 euro. La settimana successiva, sempre nel medesimo hotel, saranno ospitate invece 36 clienti che rimarranno però, solo 3 giorni. Quale sarà la previsione di entrate per quest’ultimo arrivo?

ESERCIZIO 12
L’azienda comunale che si occupa della raccolta dei rifiuti, ha pianificato che per raccogliere 250 quintali di vetro e 120 di carta, avrebbe bisogno di 120 punti di raccolta sparsi per l’abitato. Se perà volesse aumentare i quantitativi e volesse portarsi a 400 quintali di vetro e 200 di carta, quanti punti di raccolta dovrebbe organizzare?

ESERCIZIO 13
All’ufficio spedizioni delle Poste, vengono presi in carico 15 pacchi del peso di 12,5 kg ciascuno il cui costo complessivo di spedizione è di 255 euro. Il giorno successivo invece vengono presi in carico altri 30 pacchi del peso stavolta di 30 kg, quanto costerà quest’ultima operazione?

ESERCIZIO 14
In una cantina privata il vignaiolo riempie di vino rosso 360 bottiglie da 0,75 litri, svuotando un totale di 3 damigiane. Quante bottiglie da 1,8 litri sarebbero necessarie invece se volesse svuotare 6 damigiane di vino?
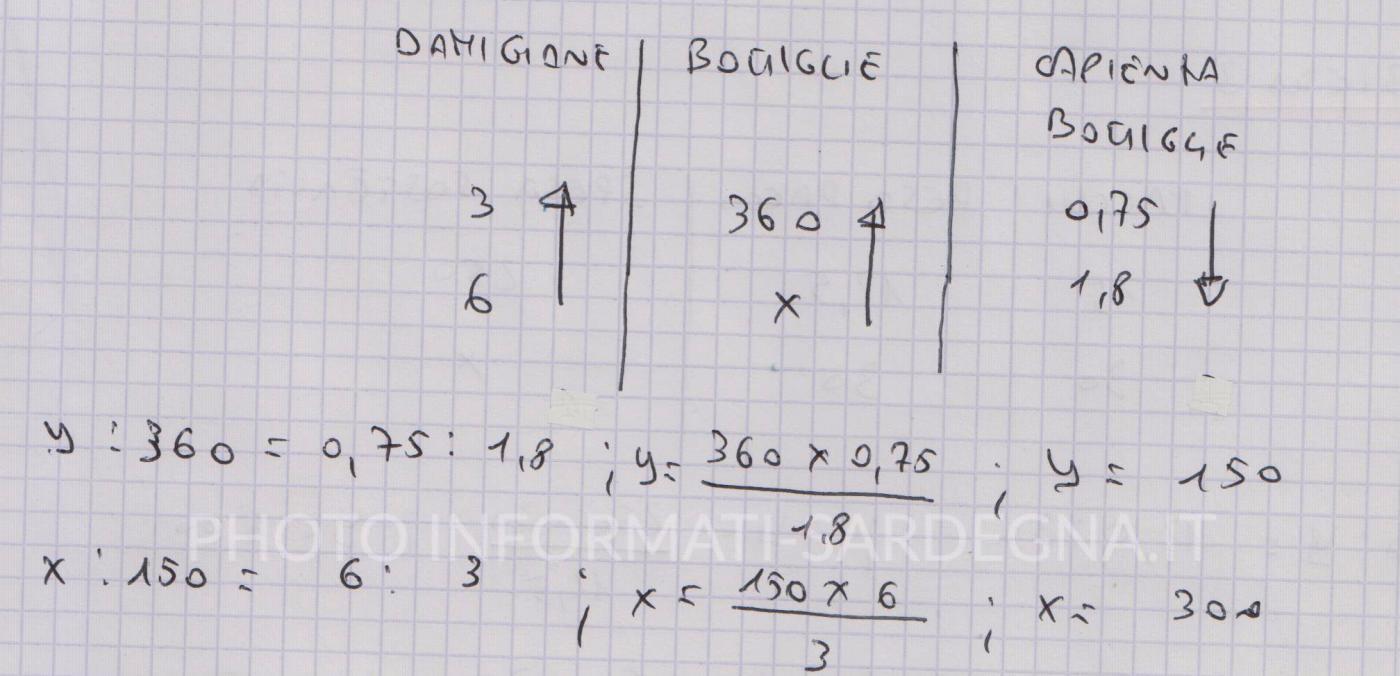
ESERCIZIO 15
Un piastrellista prepara 150 mq di mattonelle per realizzare tracciati omogenei da 0,15 metri e coprire un pavimento di 240 mq. Volesse realizzare tracciati omogenei da 0,20 metri con 300 mq di mattonelle, quanto pavimento potrebbe coprire?

ESERCIZIO 16
Un fruttivendolo spende 1000 euro per potare 30 q di frutta e verdura ad una rivendita che dista 30 chilometri dal suo terreno. Se invece porta la merce ad una rivendita che dista 6 chilometri e spende 300 euro, per rientrare nei costi quanta frutta e verdura dovrà portare?








































