La logica classica è la disciplina filosofica che studia la validità di un ragionamento dal punto di vista formale, ovvero della giusta articolazione delle sue parti.
- LEGGI ANCHE: La logica classica, test
Logica classica
Validità del ragionamento da un punto di vista formale
Il ragionamento
Un ragionamento è un insieme di proposizioni, semplici o composte, che costituiscono un discorso, un discorso razionale.
Ogni proposizione semplice è a sua volta costituita da un soggetto e da un predicato e si può legare ad altre proposizioni semplici attraverso i connettori logici per costituire delle proposizioni complesse.
L’insieme di proposizioni che costituiscono il discorso razionale è dato dal numero di predicati e il discorso è definito razionale se è in grado di determinare delle conseguenze logiche.
Ragionamento
Insieme di proposizioni
che determinano conseguenze logiche
Il criterio di verità
In logica le proposizioni sono valide, a prescindere dal significato del contenuto (semantica), solo se rispettano il criterio di verità, ovvero dicono ciò che può essere verificato come vero o falso. Altrimenti non sono proposizioni logiche.

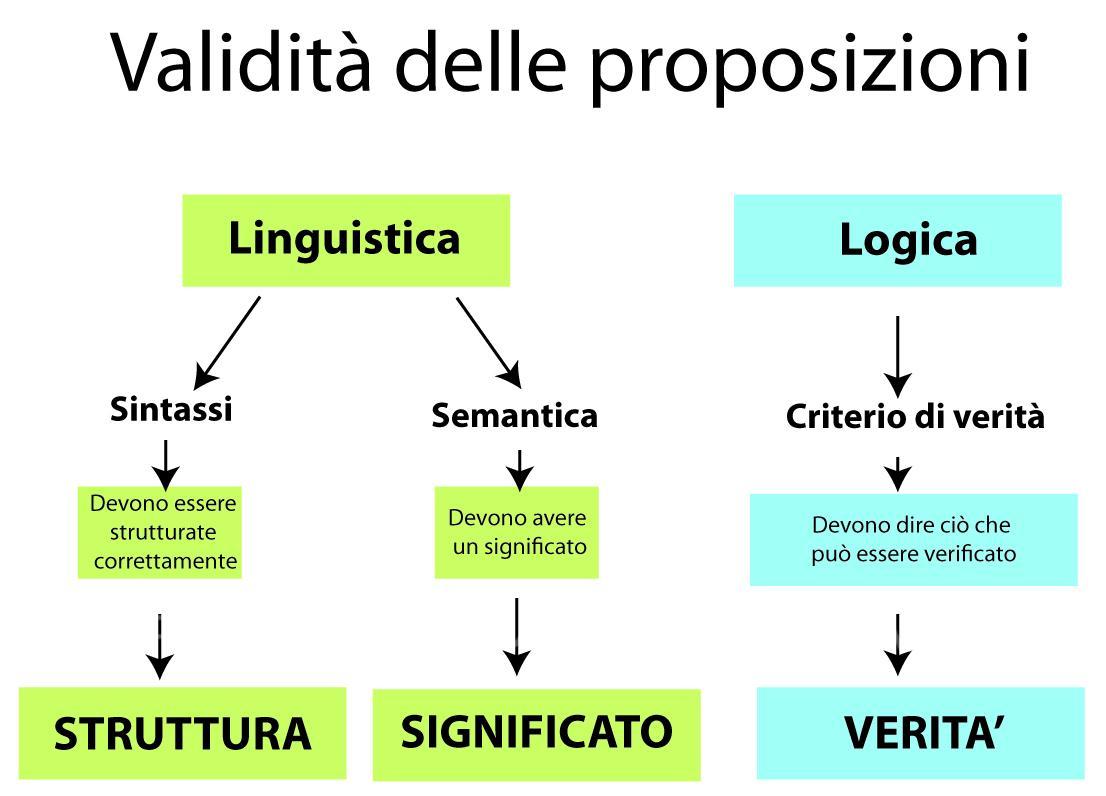
Logica e linguistica
Quindi, mentre in linguistica, affinché una proposizione sia valida è necessario che rispetti le regole della sintassi, ovvero della forma, ovvero della corretta articolazione tra le parti che la compongono (soggetto, predicato, complementi..) e della semantica (la singola frase deve esprimere un senso di fatto compiuto); in logica proposizionale la validità delle proposizioni è data dalla sintassi che deve esprimere un criterio di verità.
Validità logica e linguistica
Quindi, se dico:
- “3 è un numero dispari” è una proposizione linguisticamente corretta perché corretta nella sintassi e nella semantica, ma è anche una proposizione logicamente corretta perché può essere verificato che 3 è un numero dispari.
- “Sara è una bella ragazza” è una proposizione linguisticamente corretta nella sintassi e nella semantica, ma è illogica perché la bellezza è un criterio soggettivo non verificabile oggettivamente.
Due principi logici delle proposizioni
Le proposizioni per essere logiche oltre a rispettare i criteri di verità o di falsità devono anche rispondere a due principi:
- La proposizione è logica quando rispetta il principio di non contraddizione: una proposizione logica non può essere infatti al contempo, vera e falsa.
- La proposizione è logica quando rispetta il principio del terzo escluso: se una proposizione è falsa, allora la sua negazione è vera; viceversa se una proposizione è vera, allora la sua negazione è falsa.
Proposizioni fondamentali e secondarie
Come in linguistica, anche in logica proposizionale, all’interno di un discorso ci può essere una proposizione semplice, composta da soggetto e verbo, o una proposizione complessa, composta da più proposizioni.
Le proposizioni sono delle frasi dichiarative che hanno un senso compiuto che si reggono sul gruppo fondamentale soggetto + predicato, sufficiente da solo a formare una proposizione semplice.
Operatori logici
Gli operatori logici, o i connettivi logici, sono simboli logici (in linguistica dei simboli grammaticali) che modificano una proposizione.
Essi possono essere di due tipi:
- connettivi unari – se riguardano una sola proposizione semplice
- connettivi binari – se riguardano due o più proposizioni semplici che si legano per formare una proposizione complessa.
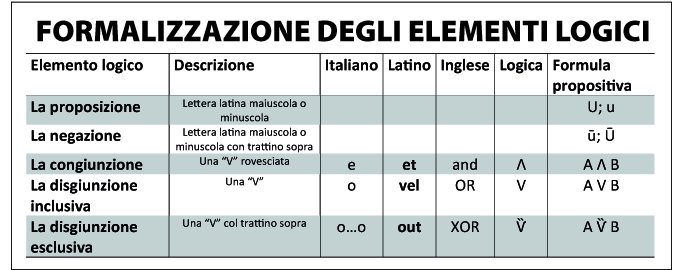
Formalizzazione
La logica per rappresentare gli elementi che studia utilizza una simbolistica precisa che è la seguente, riportata in tabella.
OPERATORE LOGICO UNARIO: LA NEGAZIONE
La negazione è l’operatore logico unario che rende falsa una frase vera e rende vera una frase falsa. La negazione dunque scambia i valori di verità e applica il principio di non contraddizione, per cui una frase se è vera non può essere falsa (e viceversa) e il principio del terzo escluso cioè non è ammessa una terza condizione al di fuori di verità o falsità . La negazione si esprime in italiano tramite la particella “non”; in inglese tramite la particella “not”, oppure in logica con un trattino sopra la lettera della proposizione (Ū; ū) o ancora (⌐U).
Ad esempio:
- Giovanni è un meccanico → U
La negazione di questa affermazione è:
- Giovanni non è un meccanico →Ū
OPERATORI LOGICI BINARI
- LA CONGIUNZIONE
- LA DISGIUNZIONE INCLUSIVA
- LA DISGIUNZIONE ESCLUSIVA
Gli operatori logici binari (o connettori logici binari) mettono a legame due o più proposizioni semplici. Per stabilire se le proposizioni complesse sono vere o false bisogna mettere a confronto i valori di verità di ogni proposizione semplice che le costituiscono e valutare, a seconda dell’operatore logico binario che le lega. Questo è possibile anche stabilirlo attraverso le tabelle della verità che sono ovviamente diverse per ogni operatore.
LA CONGIUNZIONE
La congiunzione è un operatore logico binario che serve a collegare due proposizioni semplici di pari livello gerarchico. Ad esempio, è una congiunzione di proposizione semplici:
“Giovanni è un meccanico e fa il pasticcere”
Formalizzazione della congiunzione
La congiunzione è rappresentata in italiano dalla particella “e”; in inglese con la parola “and”, oppure in logica con una V rovesciata: “É…”.
In logica, come detto, non conta il significato della proposizione ma come essa è articolata e come due o più proposizioni si legano tra loro. Quindi ad esempio, prendendo le due proposizioni semplici U e A, si ha:
- U: Giovanni è un meccanico
- A: il cane è verde
Le due proposizioni semplici è possibile legarle in una proposizione complessa attraverso l’operatore logico binario (o connettore logico binario) “e” in questo modo:
- U: Giovanni è un meccanico
- A: il cane è verde
- UÉ… A → “Giovanni è un meccanico e il cane è verde”
Criteri di verità della congiunzione
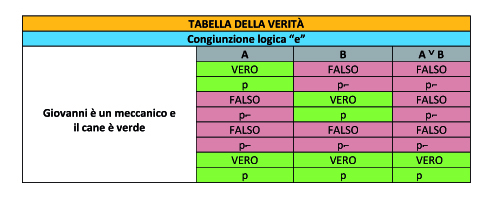
La tabella della verità di una proposizione complessa legata dall’operatore binario della congiunzione dice che la proposizione complessa è sempre falsa se una delle proposizioni semplici è falsa e se entrambe sono false. È vera invece solo se entrambe le proposizioni semplici sono vere.
Come si evince dalla seguente tabella della verità :
LE DISGIUNZIONI
Le disgiunzioni sono operatori logici binari (o connettori logici binari) che legano due o più proposizioni semplici all’interno di una proposizione complessa. Le disgiunzioni possono essere di due tipi:
La disgiunzione inclusiva → indica che ciò che viene detto nella prima proposizione può essere inclusa anche nelle altre.
La disgiunzione esclusiva → indica un’alternativa rispetto a ciò che viene detto nella prima proposizione.
La disgiunzione inclusiva
Formalizzazione della disgiunzione inclusiva
La disgiunzione inclusiva è rappresentata in italiano dalla particella “o”; in inglese dalla particella “OR”; in latino dalla particella “Vet” e in logica dal simbolo “V”.
La disgiunzione inclusiva indica che ciò che viene detto nella prima proposizione può essere inclusa anche nelle altre. Ad esempio:
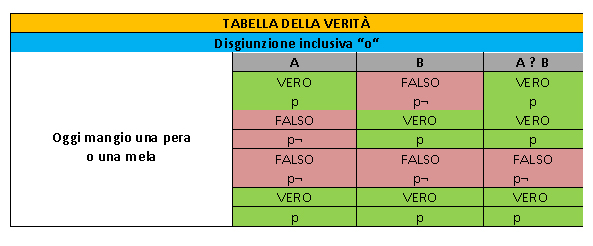
Oggi mangio una pera o una mela → Vuol dire che mangio solo una mela o solo una pera o tutte e due.
Questa disgiunzione inclusiva in logica proposizionale si rappresenta così:
- U: oggi mangio una pera;
- S: oggi mangio una mela
- UV S → Oggi mangio una pera e una mela
Criteri di verità della disgiunzione inclusiva
La disgiunzione inclusiva stabilisce che la proposizione complessa è vera se una delle due proposizioni semplici che la compongono è vera, oppure se sono vere tutte e due. Mentre è falsa nel solo caso in cui entrambe sono false.
La disgiunzione esclusiva
La disgiunzione esclusiva è un operatore logico binario (o connettore logico binario) che lega due o più preposizioni semplici all’interno di una proposizione complessa.
La disgiunzione esclusiva indica un’alternativa rispetto a ciò che viene detto nella prima proposizione semplice, ad esempio:
“Oggi o mangio una pera o mangio una mela” → Vuol dire che se mangio una pera non mangio una mela e viceversa.
Formalizzazione della disgiunzione esclusiva
La disgiunzione esclusiva è rappresentata in italiano dalle particelle “o…o”; in inglese ; in latino dalla particella “aut” e in logica dalla lettera “V” con un trattino sopra, cioè “Ñ¶”.
In logica proposizionale la proposizione “Oggi o mangio una pera o mangio una mela” viene rappresentata così:
- A: oggi mangio una pera
- B: oggi mangio una mela
- A Ѷ B → Oggi o mangio una pera o mangio una mela
Criteri di verità della disgiunzione esclusiva
La disgiunzione esclusiva può essere vera se è vera la prima e se è vera la seconda, è falsa se sono vere o se sono false entrambe.








































