 L’Insieme dei Numeri Naturali
L’Insieme dei Numeri Naturali
L’Insieme dei Numeri Naturali è l’insieme numerico più semplice perché è quello che ha il rapporto diretto con la realtà.
L’insieme dei Numeri Naturali si indica col simbolo N e comprende i numeri positivi (1,2,3, …) più lo zero (0).

L’insieme dei Numeri Naturali è infinito, ma ha un limite inferiore che è lo “zero”.
L’Addizione e la Moltiplicazione sono le uniche operazioni che è sempre possibile fare nell’Insieme dei Numeri Naturali.
La Sottrazione è possibile in N solo se il Minuendo è maggiore del Sottraendo. Questo perché in N non sono compresi i numeri negativi.
La Divisione è possibile in N solo se il Dividendo è multiplo del Divisore. Questo perché in N non sono compresi i numeri decimali.
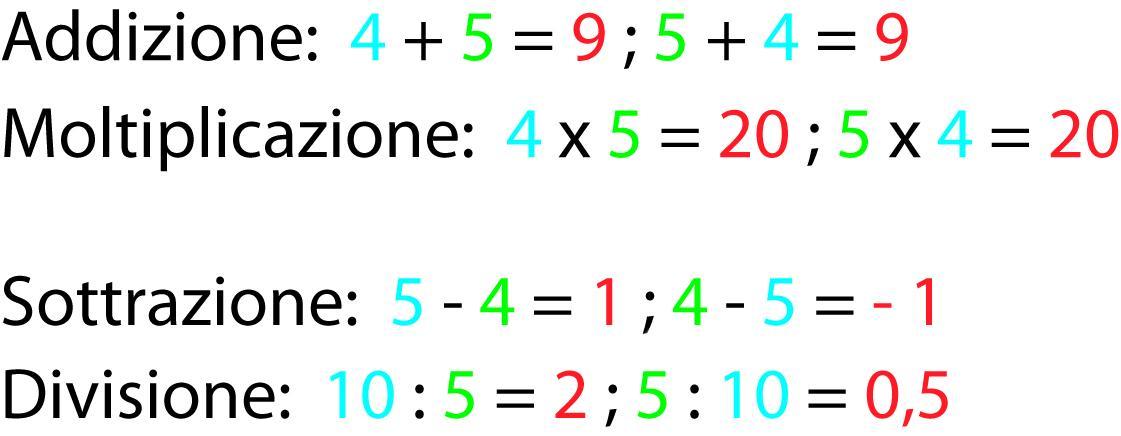

I Numeri Naturali sono detti anche Numeri Interi Positivi {1, 2, 3, 4, …} o Numeri Interi Non Negativi {0, +1, +2, +3, +4, …}.
- Numeri Naturali N = {0, 1, 2, 3, 4, …¦}
- Numeri Interi non negativi {0, +1, +2, +3, +4, …¦}
- Numeri Interi positivi {1, 2, 3, 4, …}
Lo zero nei Numeri Naturali
Secondo alcuni testi all’insieme dei Numeri Naturali (N) non appartiene lo zero perchè appartiene all’insieme dei Numeri Interi (I). Secondo altri testi lo zero invece è incluso nell’insieme dei Numeri Naturali.
La differenza nelle due interpretazioni deriva dall’utilizzo che si fa dei numeri.
- Se i numeri naturali vengono utilizzati per “contare”, ovvero si considerano numeri cardinali, allora il loro insieme include anche lo zero. Se infatti per esempio si devono contare il numero di inquilini all’interno di un condominio, è necessario rappresentare anche l’ipotesi che qualche appartamento sia vuoto, che non ci sia nessuno. In questo caso “zero inquilini”.
- Se i numeri naturali vengono utilizzati per “stabilire un ordinamento”, ovvero si considerano numeri ordinali, si esclude il numero zero. Nello stabilire ad esempio la classifica di una gara ciclistica si considera il 1° classificato, il 2° classificato, il 3° classificato … e così via, ma non si può considerare lo 0° classificato perché non c’è nessuno al 0 posto.
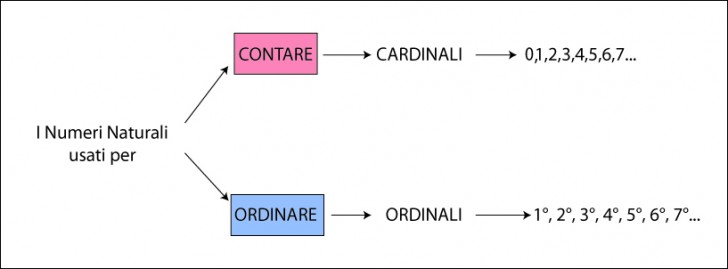
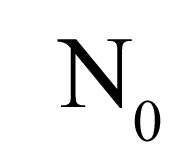
Pertanto, se nell’insieme dei Numeri Naturali includiamo lo zero, e quindi usiamo questo insieme per “contare”, il simbolo utilizzato è questo:
LEGGI ANCHE: Numeri Naturali, Test
Lo zero indica
la mancanza di oggetti
Insiemistica e Numeri Naturali
Un pastore per ricordare quante sono le pecore del suo gregge, forma un mucchio di sassolini e ad ogni sassolino fa corrispondere una pecora.
Il legame tra il sassolino e la pecora in matematica si chiama corrispondenza.
Per esemplificare in matematica si assegna una lettera agli insiemi e un numero agli elementi in essi contenuti. Quindi, in riferimento all’insieme delle pecore e all’insieme dei sassolini avremo:
- Insieme delle pecore – Insieme A
- Insieme dei sassolini – Insieme B
Contare
Se il pastore, anziché rappresentare le pecore con i sassolini, le rappresentasse direttamente con i numeri svolgerebbe un’operazione di conteggio utilizzando il concetto matematico del numero e non la rappresentazione realistica di un oggetto. Individuare il numero delle pecore del suo gregge in questo modo sarebbe dunque più semplice e più pratico piuttosto che avere il disagio di doversi procurare tanti sassolini.
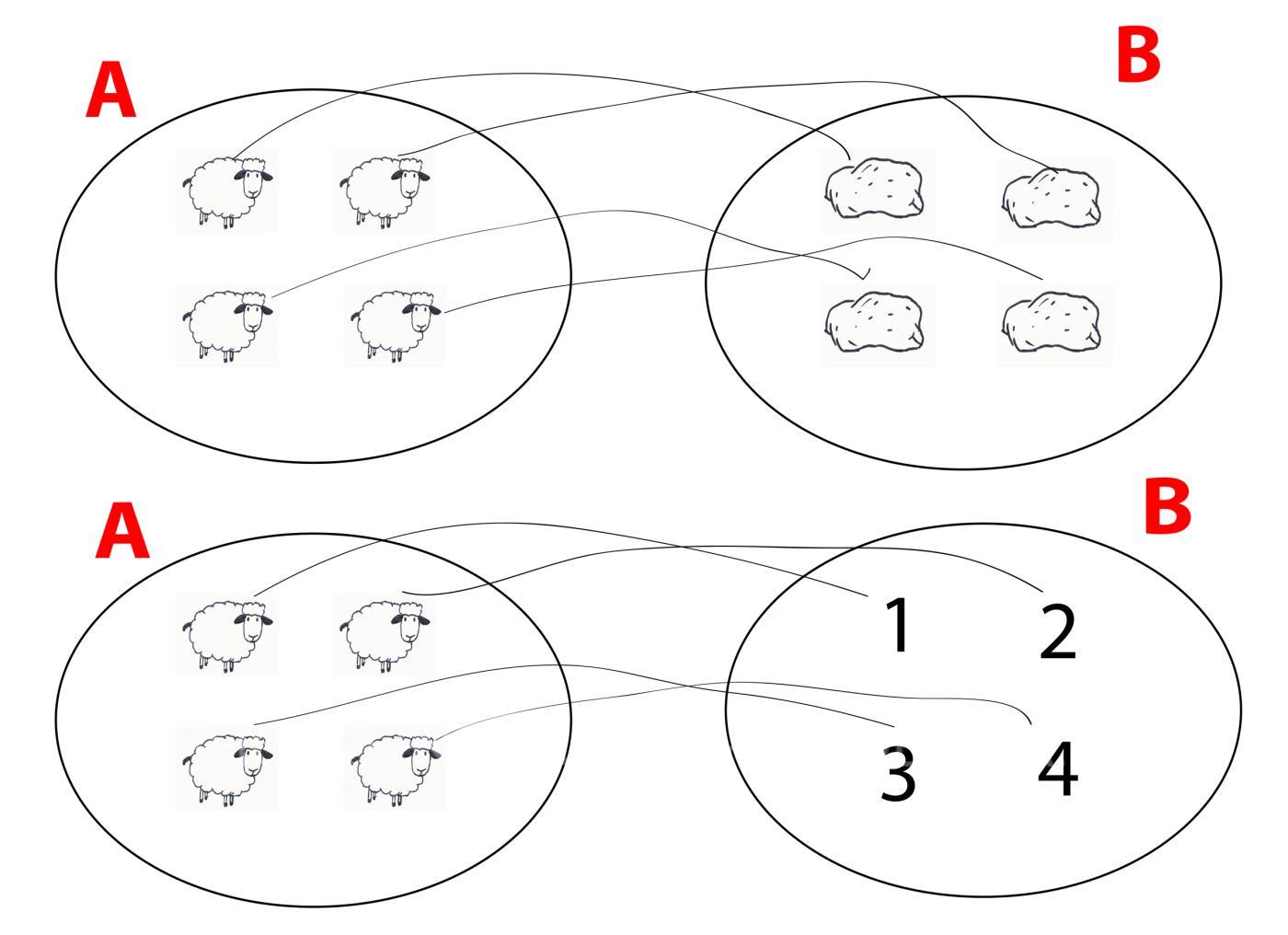
L’operazione di contare consiste dunque nello stabilire una corrispondenza tra gli oggetti che si vogliono contare (in questo caso le pecore dell’insieme A) e i numeri in ordine progressivo.
CONTARE
Stabilire una corrispondenza tra
il numero e l’oggetto
L’insieme dei Numeri Naturali
L’operazione di “conteggio” si svolge dunque stabilendo una corrispondenza, un legame o un associazione tra l’insieme degli oggetti, l’insieme A e l’insieme dei numeri, l’insieme B.
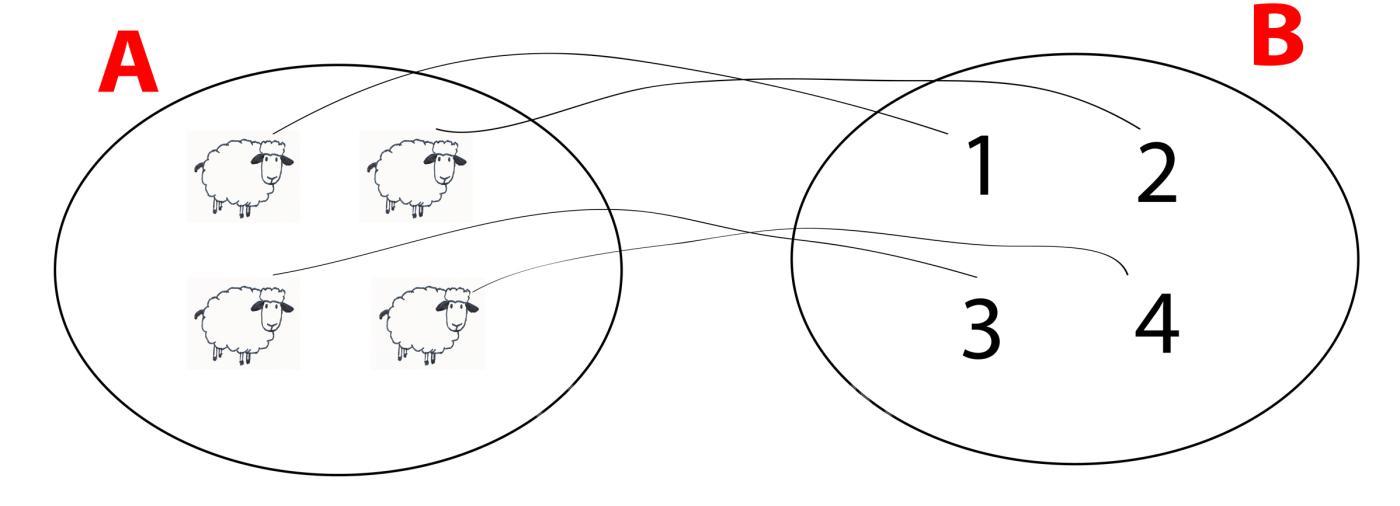
L’insieme numerico B è anche detto l’Insieme dei Numeri Naturali che inizia col numero 1 e procede all’infinito.
L’insieme è indicato con la lettera N maiuscola e si scrive così:







































