Le frazioni e i numeri decimali sono degli ampliamenti numerici dell’insieme dei numeri interi. Questi ampliamenti servono a effettuare divisioni nelle quali il dividendo non è multiplo del divisore, come ad esempio dividere un terreno fra tre eredi (1:3) o distribuire sei forme di pane tra quattro persone (6:4).
Fin dai tempi antichi dunque l’uomo ebbe la necessità di “spezzare” i numeri interi per effettuare delle divisioni in cui il dividendo non era multiplo del divisore.
- LEGGI ANCHE: Frazioni e decimali, test
Storia dei numeri decimali
L’insieme dei numeri frazionari e decimali si diffusero in due tempi diversi: prima furono gli Egizi e i Babilonesi a introdurre i numeri frazionari e, molti secoli dopo, alla fine del 1500 vennero introdotti i numeri decimali.

Frazioni e decimali sono equivalenti
Numeri frazionari e numeri decimali esprimono dunque uno stesso valore numerico in maniera diversa.
Numero decimale e frazione sono del tutto equivalenti. Pertanto:
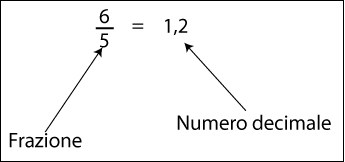
Frazioni e decimali a confronto
Frazioni e numeri decimali possono rappresentare valori equivalenti, ma non sono la stessa cosa in termini di formato. Ecco cosa li accomuna e li differenzia:
Somiglianze
- Rappresentano lo stesso tipo di quantità: sia le frazioni che i decimali possono indicare una parte di un intero.
- Esempio: 12\frac{1}{2} è equivalente a 0,50,5.
- Convertibili tra loro: una frazione può essere convertita in un numero decimale eseguendo la divisione tra numeratore e denominatore. Un numero decimale può essere riscritto come frazione (di solito semplificata).
- 34=0,75\frac{3}{4} = 0,75; 0,25=140,25 = \frac{1}{4}.
Differenze
- Formato: le frazioni si scrivono come rapporto tra due numeri (ab\frac{a}{b}), mentre i decimali usano una rappresentazione con la virgola o il punto (0,250,25).
- Tipi di valori rappresentabili: alcune frazioni non hanno una rappresentazione decimale esatta, come 13\frac{1}{3}, che diventa 0,333…0,333…, un decimale periodico.
- Uso pratico: le frazioni sono utili in contesti matematici o teorici (esempio: esprimere rapporti o proporzioni esatte), mentre i decimali sono spesso preferiti per calcoli e misurazioni.
Quindi, frazioni e decimali possono rappresentare lo stesso valore, ma il modo in cui lo fanno è diverso.
I numeri decimali
Nel Sistema di Numerazione Decimale il valore delle cifre è dato dalla posizione che esse hanno all’interno del numero.
LA COMPONENTE INTERA DEL NUMERO
La parte intera del numero si compone nel seguente modo:
- A destra si trova l’ordine dell’unità più semplice
- A sinistra man mano si aggiungono le cifre degli ordini più grandi (decine, migliaia, centinaia…)
- Passando da un ordine più piccolo ad uno più grande il valore della cifra precedente viene moltiplicato per dieci.
Ciò significa che il Sistema di Numerazione attualmente usato, il Sistema di numerazione indo-arabo è di tipo posizionale su base 10

La componente decimale
Quando si vuole rappresentare il numero oltre che nella sua componente intera anche in quella decimale, a destra della cifra dell’ordine dell’unità si appone la virgola e quindi a seguire le cifre dell’ordine dei decimi, dei centesimi, dei millesimi etc. Queste cifre a destra della virgola vengono chiamate unità decimali.

Per quanto riguarda le cifre decimali, esse diminuiscono di valore man mano che si passa dall’ordine dei decimali, a quelli dei centesimi, dei millesimi e così via. La diminuzione avviene dividendo per dieci il valore dell’unità precedente. Quindi:
- 1 unità vale 1/10 di unità ;
- 1 centesimo vale 1/100 di unità ;
- 1 millesimo vale 1/1000 di unità …
Viceversa, le cifre della componente intera aumentano di 10 ogni volta che si passa da un ordine più piccolo ad uno più grande. Ovvero:
- per fare una unità servono 10 decimi
- per fare una decina servono 10 unità
- per fare un centinaio servono 100 unità o 10 decine
- per fare un migliaio servono 1000 unità o 10 centinaia
LE FRAZIONI
Frazionare significa “dividere in parti uguali”.
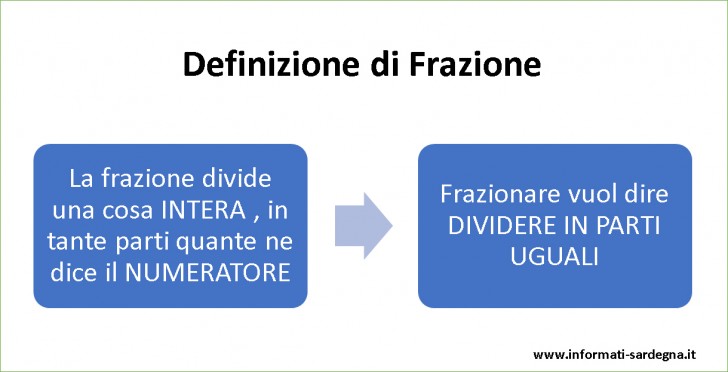
TIPI DI FRAZIONI
In matematica le frazioni possono essere classificate in due modi:
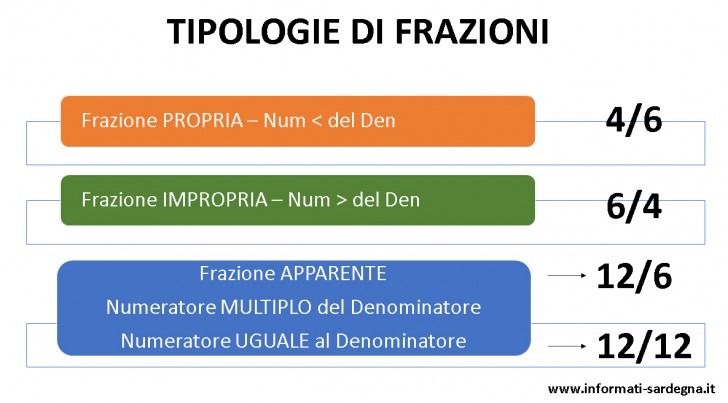
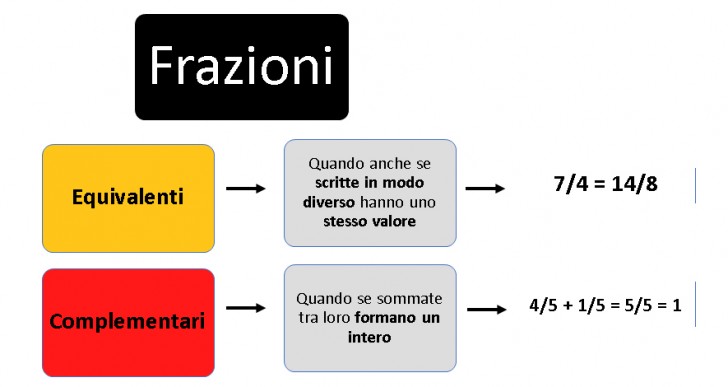
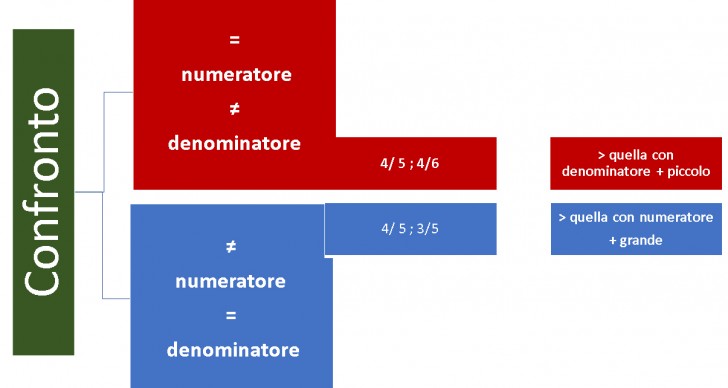
- LEGGI ANCHE: Problemi con le frazioni
Da numero decimale a frazione
- Scrivi il numero decimale come un rapporto:
- Ad esempio, 0,750,75 diventa 75100\frac{75}{100}.
- Semplifica la frazione:
- Trova il massimo comune divisore (MCD) tra numeratore e denominatore.
- Nel nostro esempio:
7575 e 100100 hanno un MCD di 2525.
75100=75÷25100÷25=34\frac{75}{100} = \frac{75 \div 25}{100 \div 25} = \frac{3}{4}.
- Verifica: Controlla che il risultato sia corretto rifacendo la divisione.
- 34=0,75\frac{3}{4} = 0,75.
Da frazione a numero decimale
- Esegui la divisione:
- Dividi il numeratore (sopra) per il denominatore (sotto).
- Ad esempio:
34=3÷4=0,75\frac{3}{4} = 3 \div 4 = 0,75.
- Decimali periodici:
- Alcune frazioni hanno una divisione che non si interrompe mai, come 13=0,333…\frac{1}{3} = 0,333\ldots (decimale periodico).
- In tal caso, puoi indicare il risultato come 0,3‾0,\overline{3}.
Esempi pratici
- Da 0,20,2 a frazione:
- 0,2=2100,2 = \frac{2}{10}, semplificato: 15\frac{1}{5}.
- Da 78\frac{7}{8} a decimale:
- 7÷8=0,8757 \div 8 = 0,875.
Autore dell’Articolo: Pierpaolo Spanu








