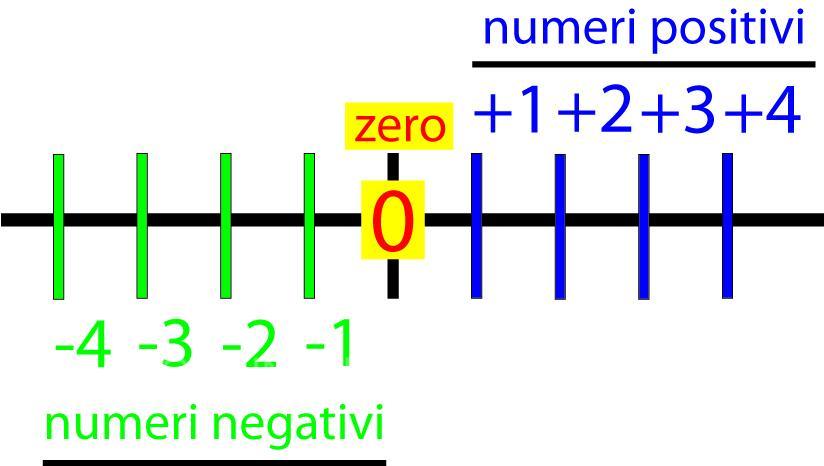
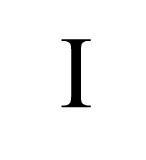I Numeri Interi sono un’estensione dei Numeri Naturali perché compredono oltre ai numeri positivi e allo zero, anche i numeri negativi.
I Numeri Interi sono simboleggiati dalla lettera “i” maiuscola
Operazioni nell’Insieme dei Numeri Interi
Nell’Insieme dei Numeri Interi è possibile svolgere le operazioni di Addizione, di Moltiplicazione e Sottrazione.
Comprendendo infatti i numeri interi negativi, è possibile effettuare – sempre – anche l’operazione di Sottrazione.
L’operazione della Divisione invece, non è sempre possibile nell’Insieme dei Numeri Interi, perché qualora vi fosse il caso di un Dividendo che non è multiplo del Divisore, l’Insieme dei Numeri Interi non comprende i Numeri Decimali.
Inclusione dei Naturali negli Interi
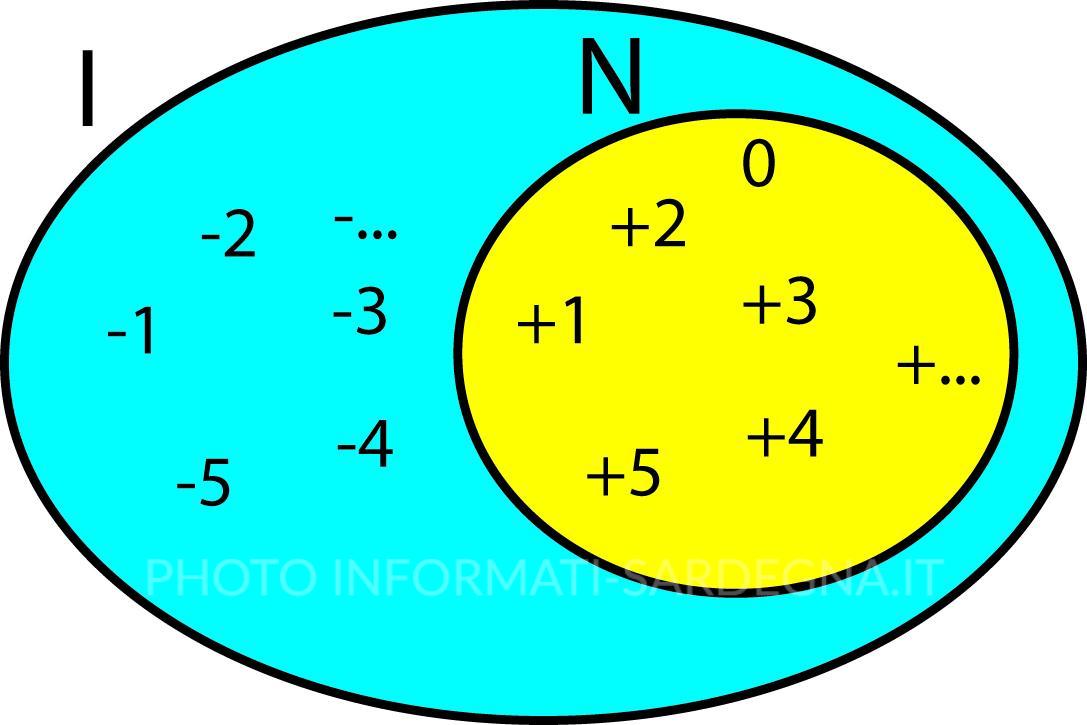
L’Insieme dei Numeri Interi è dunque un allargamento dell’Insieme dei Numeri Naturali. Pertanto, utilizzando il linguaggio insiemistico si può dire che l’Insieme dei Numeri Naturali è incluso nell’Insieme dei Numeri Interi.
N ⊂ I – che si legge: l’Insieme dei Numeri Naturali è incluso nell’Insieme dei Numeri Interi
Utilizzando una rappresentazione grafica si può disegnare la relazione tra Numeri Naturali e Numeri Interi utilizzando la Rappresentazione di Venn
- LEGGI ANCHE: La Teoria degli Insiemi
