5 / A – Divisioni con la virgola

Le divisioni con la virgola, dette anche divisioni con i numeri decimali, mettono solitamente in difficoltà gli studenti perchè richiedono delle procedure di calcolo più complesse rispetto alle divisioni con numeri senza la virgola, dette queste ultime divisioni con i numeri interi.

LEGGI ANCHE: LA DIVISIONE

A seguire le tre casistiche che si possono incontrare nel dover svolgere delle operazioni di divisione con numeri con la virgola.

Casi:

1. Numero con la virgola al dividendo;
2. Numero con la virgola al divisore;
3. Numero con la virgola al dividendo e al divisore.

CASO 1 – NUMERO CON LA VIRGOLA AL DIVIDENDO

• Esempio: risolvere la divisione 34,3:3

Procedura di svolgimento:

1. Spostare la virgola del dividendo verso destra, tante volte quante sono le cifre che stanno a destra della stessa. Quindi: 34,3 →343
2. Aggiungere al divisore tanti zeri quante volte sono le volte in cui è stata spostata verso destra la virgola del dividendo. Quindi 3 →30
3. Svolgere la divisione dei numeri ottenuti: 343:30. Il risultato ottenuto sarà lo stesso della divisione 34,3:3

CASO 2 – NUMERO CON LA VIRGOLA AL DIVISORE

• Esempio: risolvere la divisione 343: 3,3

Procedura di svolgimento:

1. Togliere la virgola del divisore
2. Aggiungere tanti zeri al dividendo quante erano le cifre del divisore oltre la virgola
3. Procedere alla divisione delle cifre ottenute (3430:33), il cui risultato è identico alla divisione 343:3,3

• Esempio: risolvere la divisione 127: 34,72

– Questa divisione con il numero con la virgola al divisore, ha la particolarità di avere complessivamente più cifre rispetto al divisore –

Procedura di svolgimento:

1. Spostare la virgola del numero del divisore, tante volte quante sono le cifre dopo la stessa. Quindi: 34,72 → 3472;
2. Aggiungere tanti zeri al dividendo, quante sono le cifre del divisore che stanno oltre la virgola. Quindi: 127 →12700
3. Svolgere la divisione: 12700:3472, il cui risultato equivale alla divisione 127:34,34

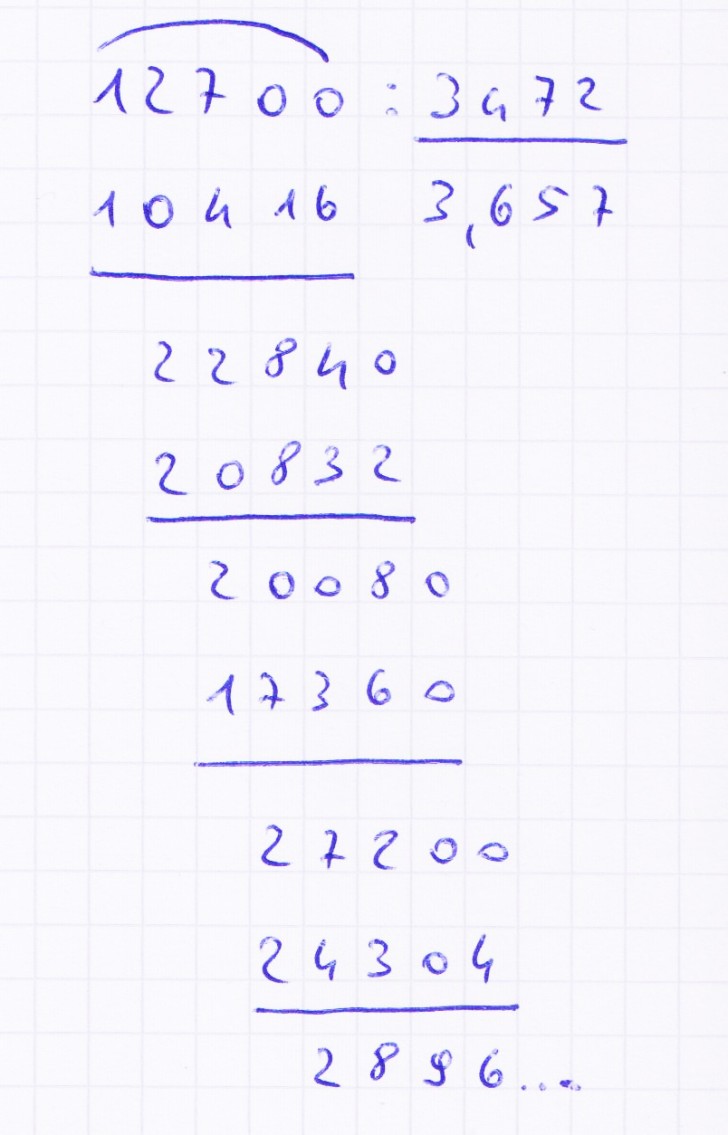
CASO 3 – NUMERO CON LA VIRGOLA AL DVIDENDO E AL DIVISORE

• Esempio: risolvere la divisione 57,57: 4,3

In questo caso decide la virgola al divisore perchè non si può eseguire una divisione con la virgola al divisore, dobbiamo applicare la proprietà invariantiva, quella che dice che “se dividiamo o moltiplichiamo entrambi i termini della divisione (dividendo e divisore) per uno stesso numero, il quoziente o il quoto non cambiano”.

1. Togliere la virgola del divisore moltiplicandolo per 10 (in questo caso). Ovvero: 4,3×10 = 43
   
2. Spostare la virgola del dividendo moltiplicando anche questo numero per la medesima cifra (10) = 57,57×10 = 575,7
   
3. Calcolare quante volte il 43 sta nel 575, ovvero: 13 volte. Questa cifra la aggiungo dopo la virgola ed effettuo la moltiplicazione col 43
   A questo punto effettuo la sottrazione di 575 per 559 e ottengo 167
4. Aggiungo la virgola dopo il 13
   
5. Calcolo quante volte il 43 sta nel 167, ovvero: 3 volte. Questa cifra la aggiungo dopo la virgola ed effettuo la moltiplicazione col 43
   
6. A questo punto devo effettuare la sottrazione tra 167 e 129 e ottengo 38
   
7. Ora lavoro sui centesimi e vedendo che il 38 è più piccolo del 43 gli aggiungo uno 0 a destra e ottengo il 380. Calcolo ora quante volte il 43 sta nel 480. Ovvero: 8 volte

Si arriva così alla conclusione che 57,57:4,3 equivale, applicando la proprietà invariantiva a divisore per togliere la virgola, alla divisione 575,5:43

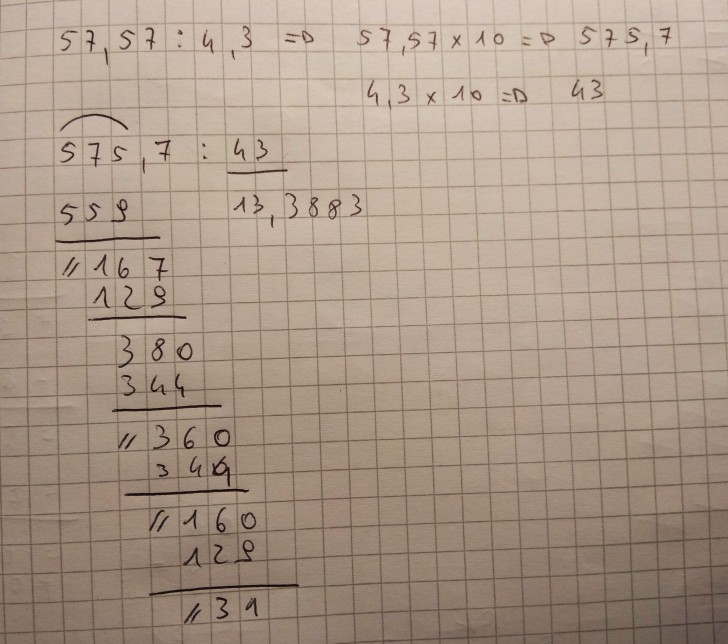
Autore dell’articolo: Pierpaolo Spanu