La Teoria degli insiemi è la teoria matematica che utilizza il concetto di insieme nel linguaggio logico-matematico.
- LEGGI ANCHE: Esercizi sugli Insiemi
L’insieme matematico è un raggruppamento di elementi che è possibile stabilirlo univocamente e oggettivamente perché hanno una caratteristica comune.
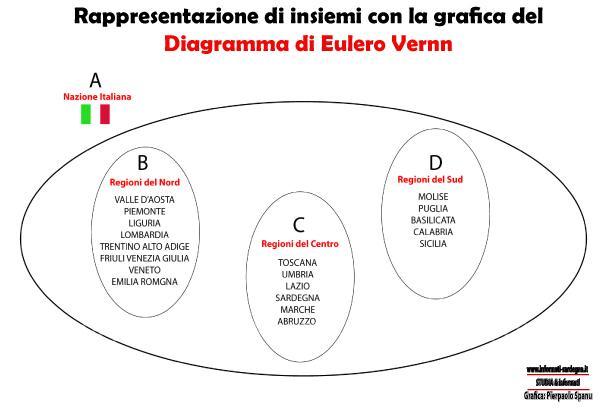
Prendere ad esempio l’insieme delle regioni d’Italia e chiedersi se la regione del Kossovo faccia parte o meno di questo insieme significa fare un ragionamento logico-matematico con la teoria degli insiemi.
- LEGGI ANCHE: Teoria degli Insiemi, Test
Teoria degli Insiemi, gli argomenti
- Concetto di insieme
- Gli elementi dell’insieme
- La rappresentazione dell’insieme
- L’appartenenza
- Il sottoinsieme: l’insieme proprio e l’insieme improprio
- L’inclusione
- L’intersezione
- La disgiunzione
- L’uguaglianza degli insiemi
- L’insieme vuoto
- L’insieme universo
- L’insieme finito
- L’insieme infinito
- Gli insiemi disgiunti
- L’insieme complementare
- L’insieme delle parti
- La partizione insieme
- Il prodotto cartesiano
- La rappresentazione cartesiana
- Le operazioni tra gli insiemi: l’intersezione, unione, la differenza
Definizione di insieme
Un insieme è un concetto primitivo che definisce un raggruppamento qualsiasi di elementi che hanno una caratteristica in comune.
Rappresentazione di un insieme
L’insieme si rappresenta con la scrittura o con la grafica.
La rappresentazione con la scrittura avviene in due modi:
- Rappresentazione per elencazione
- Rappresentazione per proprietà caratteristica
La rappresentazione grafica avviene in un modo:
- Rappresentazione col Diagramma di Eulero Venn
La rappresentazione per Elencazione si utilizza quando sono pochi gli elementi da elencare
La rappresentazione per Proprietà Caratteristica si utilizza quando si vuole rappresentare la proprietà specifica degli elementi di quell’insieme
La rappresentazione di Eulero Venn si utilizza per dare un’idea visiva chiara dell’insieme
Linguaggio della Teoria degli Insiemi
Nel linguaggio della Teoria degli Insiemi
- gli Elementi si identificano con la lettera minuscola
- gli Insiemi si identificano con la lettera maiuscola

Simboli della Teoria degli Insiemi
I simboli della Teoria degli Insiemi sono i seguenti
Appartenenza
Definizione di appartenenza
Quando un elemento è contenuto nell’insieme, si parla di appartenenza. L’appartenenza si rappresenta graficamente con il simbolo di appartenenza.
Mentre la non appartenenza di un elemento ad un insieme, qualora non avesse le caratteristiche di comunanza a quel determinato insieme, si rappresenta con il simbolo di non appartenenza.

L’appartenenza o la non appartenenza si leggono con le seguenti scritture insiemistiche:

La relazione tra gli insiemi
La relazione tra gli insiemi è la corrispondenza che si stabilisce tra gli elementi di un insieme e gli elementi di un altro insieme.
Questa corrispondenza si stabilisce sulla base delle proprietà tra gli elementi.
Il sottoinsieme
Dati due insiemi A e B, si dice A sottoinsieme di B quando gli elementi di A fanno parte del sovrainsieme B.
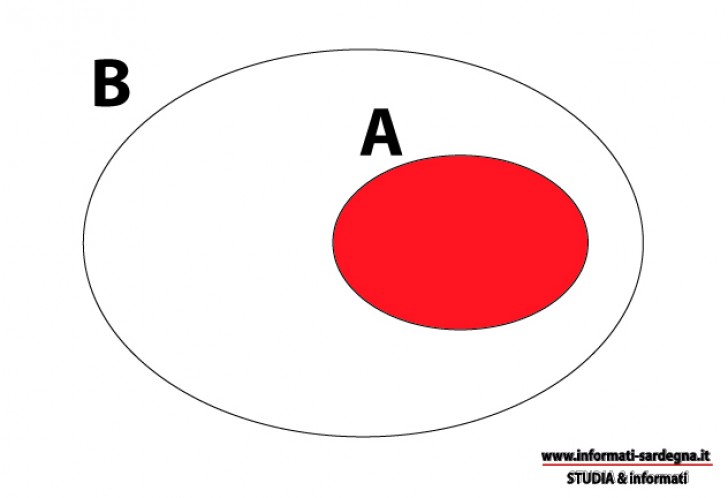
Per indicare che A è sottoinsieme di B si usa la seguente scrittura
L’inclusione
Definizione di inclusione
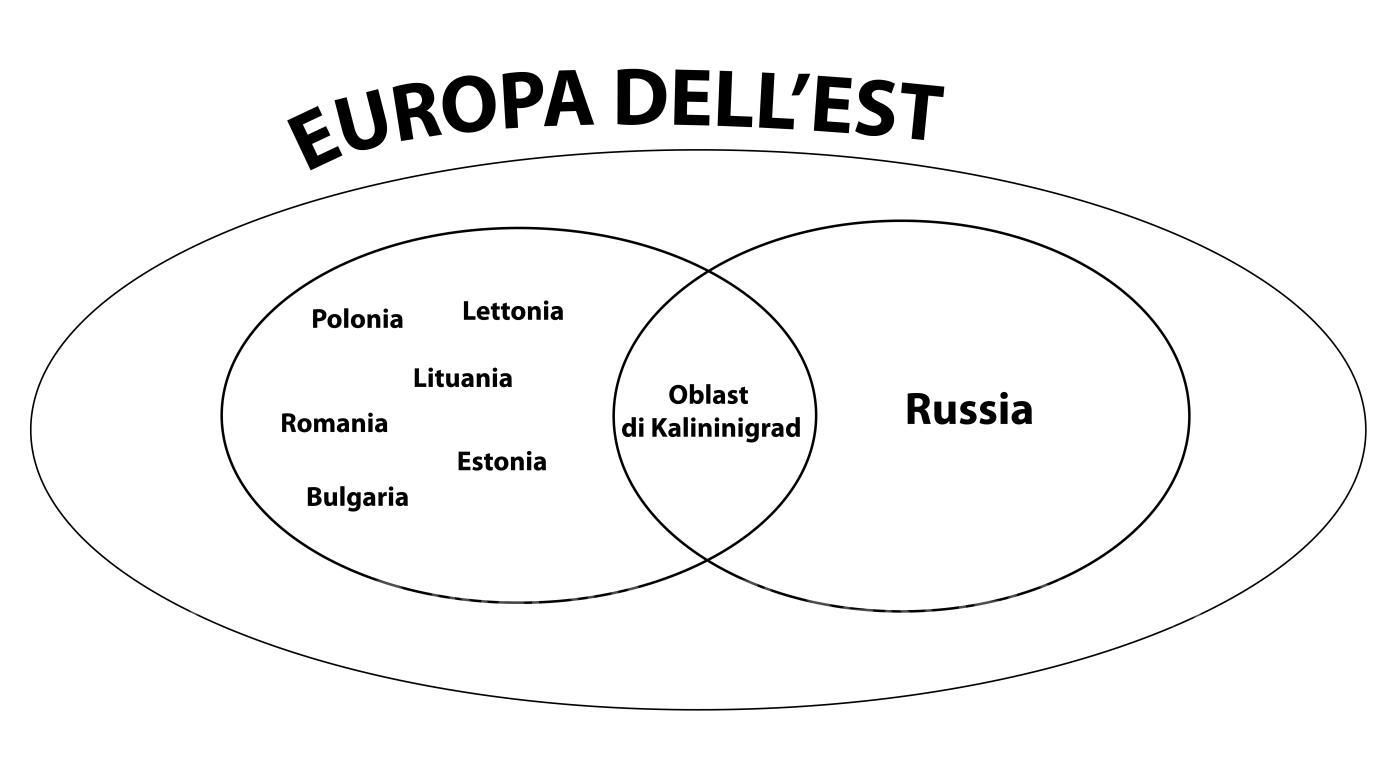
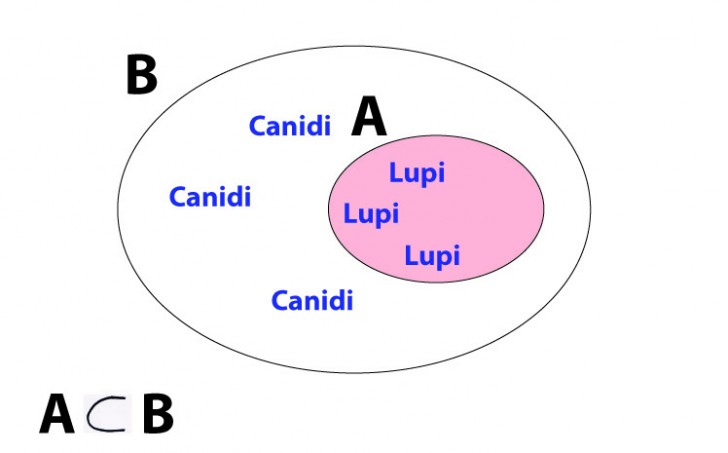
L’inclusione è una relazione tra due insiemi, di cui uno è contenuto nell’altro.
L’insieme che contiene si chiama sovrainsieme, l’insieme che è contenuto si chiama sottoinsieme. uno detto sovrainsieme e un sottoinsieme.
In figura l’insieme A è il sottoinsieme, contenuto nell’insieme B, il sovrainsieme.
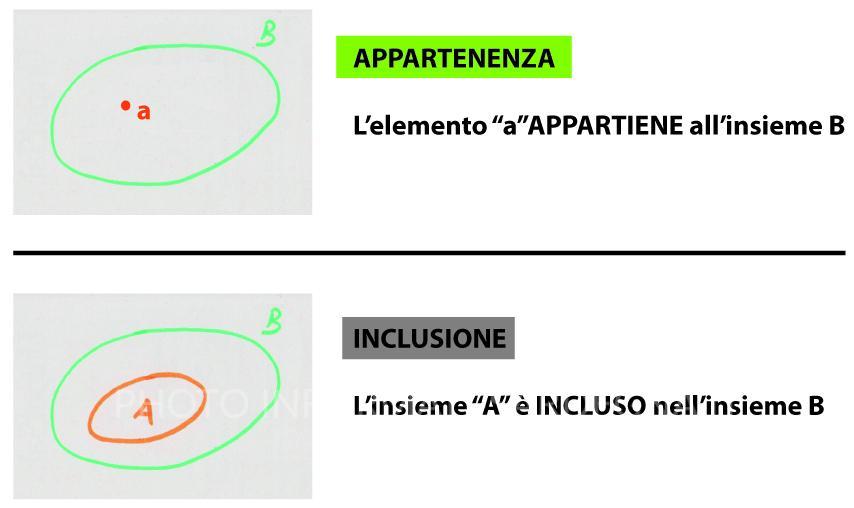
Differenza tra Appartenenza e Inclusione
- L’Appartenenza definisce la relazione tra un elemento e l’insieme, ovvero, quando un elemento è contenuto nell’insieme, si parla di appartenenza.
- L’Inclusione definisce la relazione tra due insiemi, ovvero, quando un insieme è contenuto nell’insieme più grande, si parla di inclusione.
Inclusione stretta e inclusione normale
La Teoria degli Insiemi prevede però che esistano due tipi di sottoinsieme e due tipi di inclusione:
- l’Inclusione Stretta, avviene quando tutti gli elementi di A fanno parte di B, ma non viceversa;
- l‘Inclusione Normale, avviene quando quando tutti gli elementi di A fanno parte di B e viceversa.
Ciò significa che nell’Inclusione Normale è prevista anche l’uguaglianza tra sovrainsieme e sottoinsieme; mentre nell’Inclusione Stretta gli elementi di sovrainsieme e sottoinsieme sono diversi.

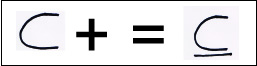 Inclusione Normale e Inclusione Stretta vengono rappresentati coi simboli qui sopra e come si nota nel simbolo di Inclusione Normale sotto la “c” schiacciata c’è un trattino che indica l’uguale.
Inclusione Normale e Inclusione Stretta vengono rappresentati coi simboli qui sopra e come si nota nel simbolo di Inclusione Normale sotto la “c” schiacciata c’è un trattino che indica l’uguale.
Mentre nel simbolo dell’Inclusione Stretta gli insiemi hanno elementi di diversità in quanto, come detto, gli elementi del sottoinsieme possono essere anche gli stessi dell’sovrainsieme ma non viceversa.
Esempi di Inclusione stretta e Inclusione normale

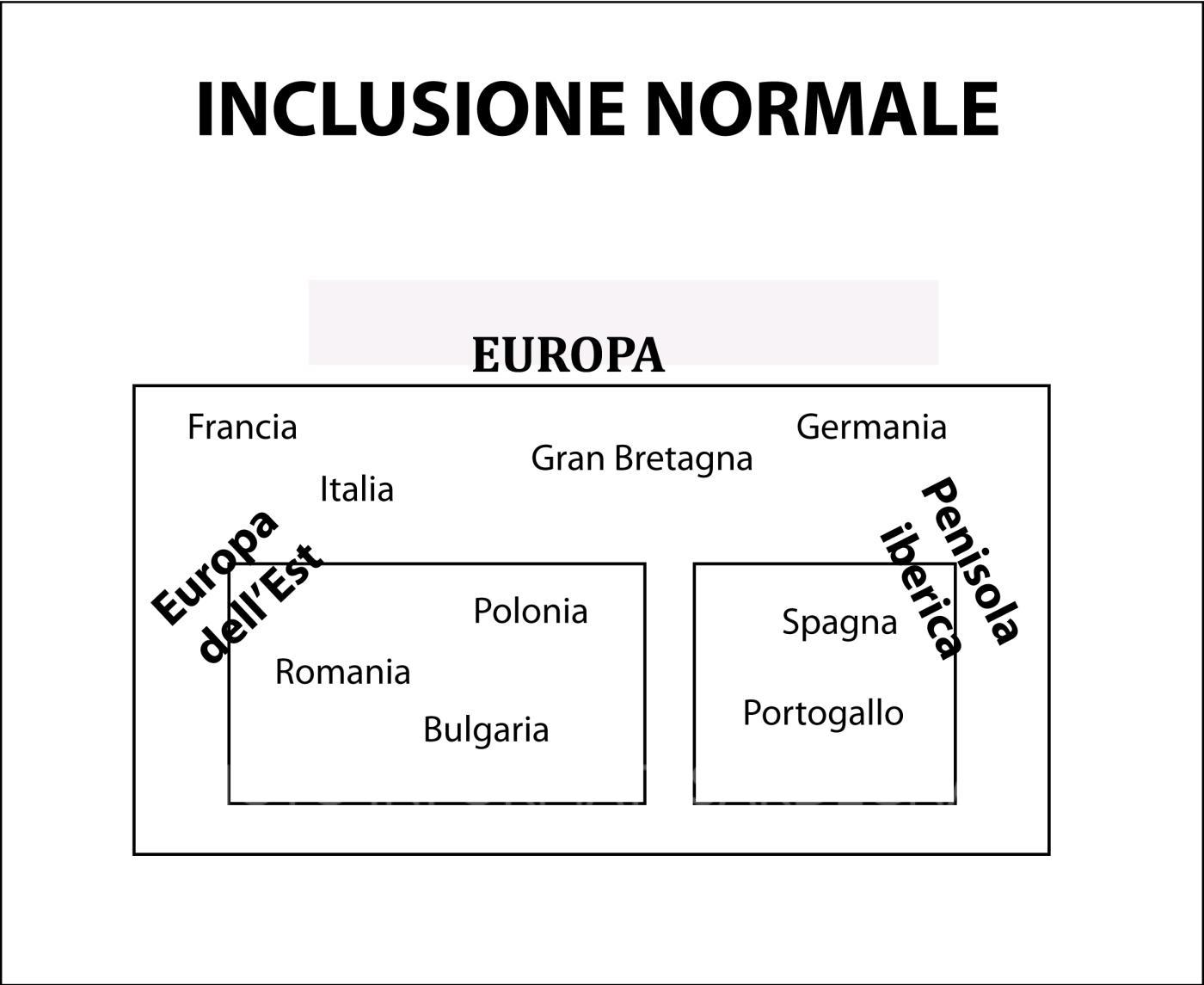
Sottoinsieme proprio e Sottoinsieme improprio
Definizione di Sottoinsieme Proprio
Un Sottoinsieme Proprio è un sottoinsieme che ha un rapporto di Inclusione Stretta col sovrainsieme, questo perché gli elementi contenuti nel sottoinsieme appartengono al sovrainsieme ma non viceversa.

Definizione di Sottoinsieme Improprio
Un Sottoinsieme Improprio è un sottoinsieme che ha un rapporto di Inclusione Normale col sovrainsieme, perchè gli elementi contenuti nel sottoinsieme sono uguali a quelli contenuti nel sovrainsieme.

L’insieme vuoto è un’inclusione normale
o un sottoinsieme improprio
L’insieme vuoto è un sottoinsieme di qualsiasi insieme, esso pertanto è un sottoinsieme improprio di ogni altro insieme, in quanto ogni elemento dell’insieme vuoto, cioè nessun elemento, appartiene a se stesso. Quindi, l’unico sottoinsieme dell’insieme vuoto è se stesso.

Si parla dunque di:
- sottoinsieme proprio quando gli insiemi sono parzialmente diversi
- sottoinsieme improprio quando gli insiemi sono uguali
Intersezione
Definizione di intersezione
L’intersezione di insiemi è l’insieme formato dagli elementi comuni a due o più insiemi.
Il simbolo dell’intersezione è una “U” rovesciata

L’intersezione può essere rappresentata graficamente con il diagramma di Eluero Venn qui sotto:
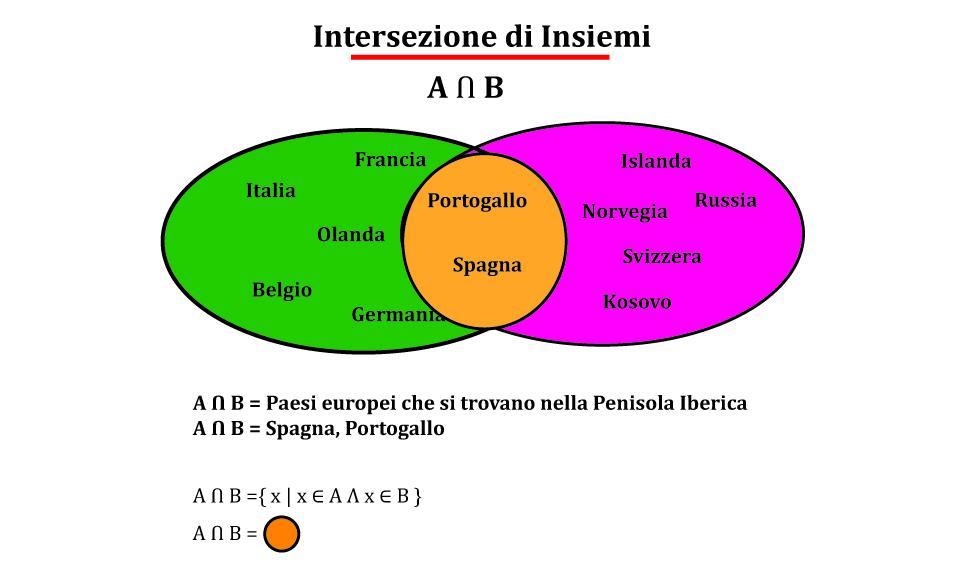
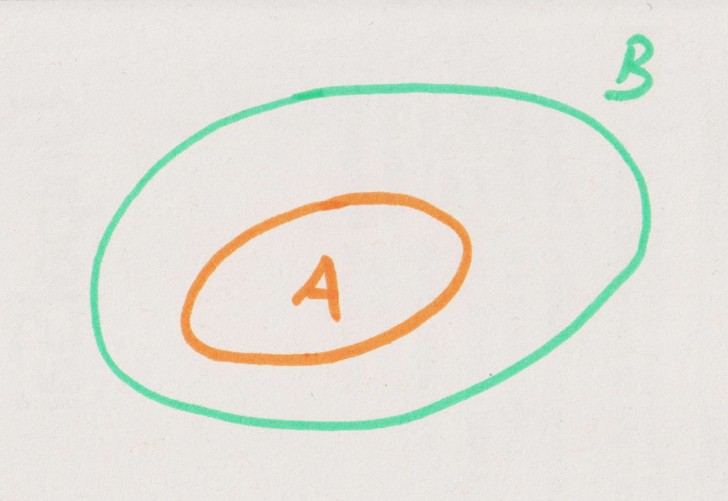
L’inclusione stretta (o sottoinsieme proprio) e l’intersezione
Nel caso in cui si verifichi una situazione di “inclusione stretta” e “sottoinsieme proprio”, dove cioè un insieme è incluso in un altro (vedi figura in basso), si può ugualmente parlare di “Intersezione”, ovvero che:
B ∩ A = B
Disgiunzione
Definizione di disgiunzione tra insiemi
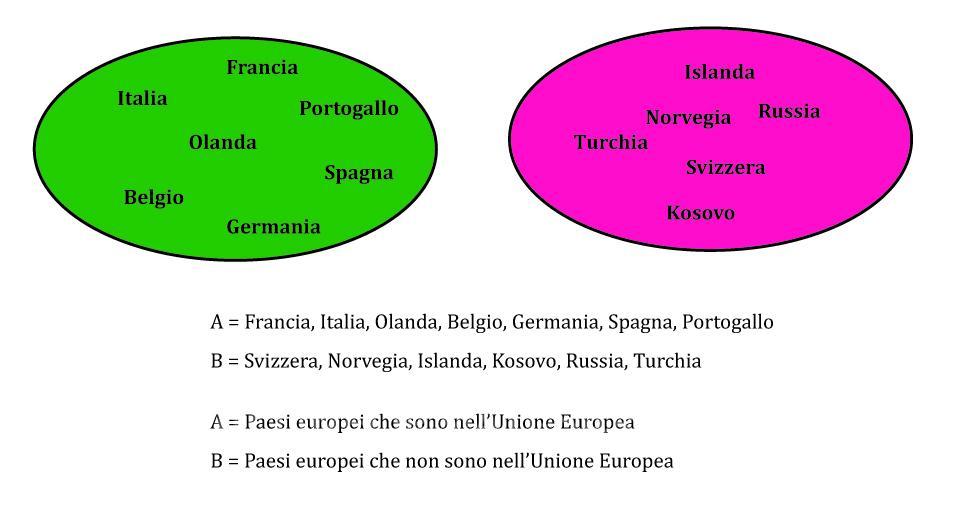
Quando due o più insiemi non hanno elementi in comune si parla di insiemi disgiunti.
La disgiunzione è pertanto il contrario dell’uguaglianza e viene rappresentata attraverso il diagramma di Eulero Venn nel seguente modo:
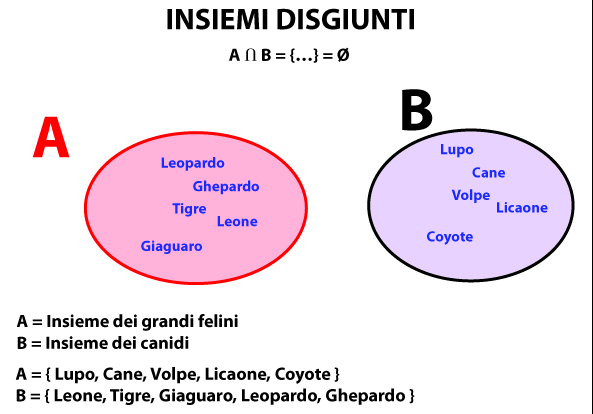
La scrittura per elencazione di
insiemi disgiunti è la seguente:
A ∩ B = {Ø}
Uguaglianza
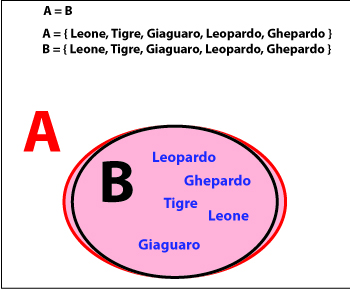
Definizione di uguaglianza tra insiemi
L’uguaglianza è una relazione in cui due o più insiemi hanno gli stessi elementi, ovvero quando l’insieme A, ha gli stessi elementi dell’insieme B (o C, o D…).
La relazione di uguaglianza si rappresenta con la seguente notazione matematica dell’uguale (=).
Gli insiemi hanno una reciproca relazione di inclusione o una doppia inclusione che può essere rappresentata dal diagramma di Eulero Venn qui a destra.
Relazioni
- Inclusione stretta → Sottoinsieme proprio → Intersezione
- Inclusione normale → Sottoinsieme improprio → Uguaglianza
Un rapporto di Inclusione stretta da due insiemi prevede l’esistenza di un sottoinsieme proprio e l’intersezione di questo con il suo sovrainsieme.
Quindi: A ⊂ B → A ∩ B
Un rapporto di Inclusione normale tra due insiemi prevede l’esistenza di un sottoinsieme improprio e l’uguaglianza di questo col suo sovrainsieme
Quindi: A ⊆ B → A = B
Unione
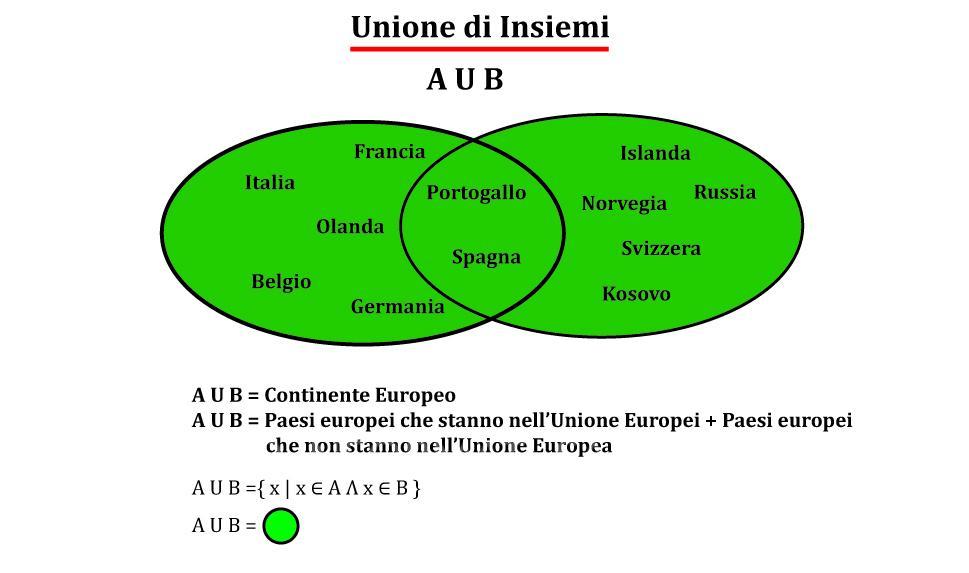
Definizione di unione tra insiemi
L’unione di due o più insiemi è l’insieme che comprende tutti gli elementi degli insiemi in un unico insieme

Differenza tra Insiemi
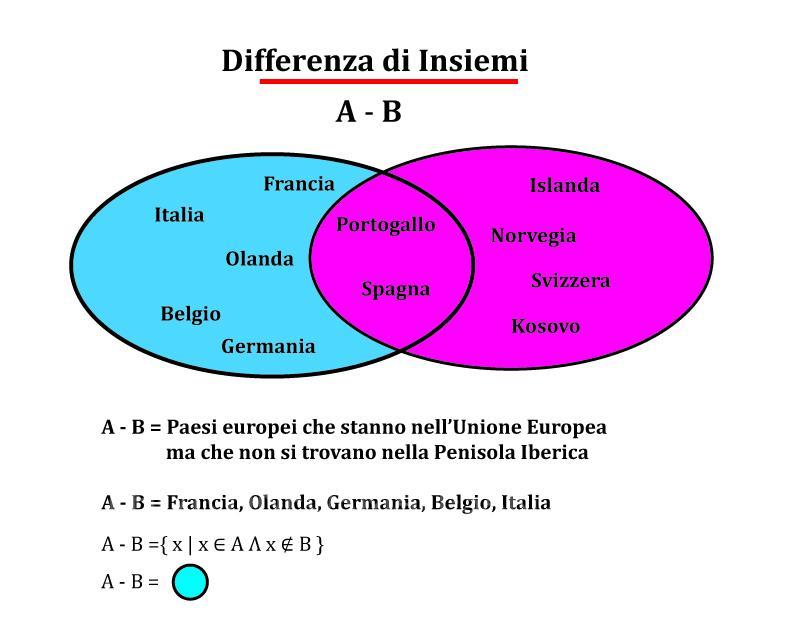
Definizione di differenza
Si dice differenza tra due insiemi A e B, l’insieme degli elementi di A che non appartengono a B
La Differenza si può applicare ai concetti di Intersezione, di Inclusione e di Disgiunzione.

A confronto
Unione, Intersezione e Differenza di Insiemi
Concetti insiemistici
- L’INSIEME VUOTO → L’insieme vuoto (Ø ) è l’insieme che non ha elementi
- L’INSIEME UNIVERSO → L’insieme universo (U) è l’insieme a cui appartengono tutti gli elementi degli insiemi che esistono.
- L’INSIEME FINITO → L’insieme finito (i) è l’insieme che comprende un numero determinato di elementi
- L’INSIEME INFINITO → L’insieme infinito (I) è l’insieme che comprende un numero indeterminato di elementi
Insiemi complementari
Definizione di insieme complementare
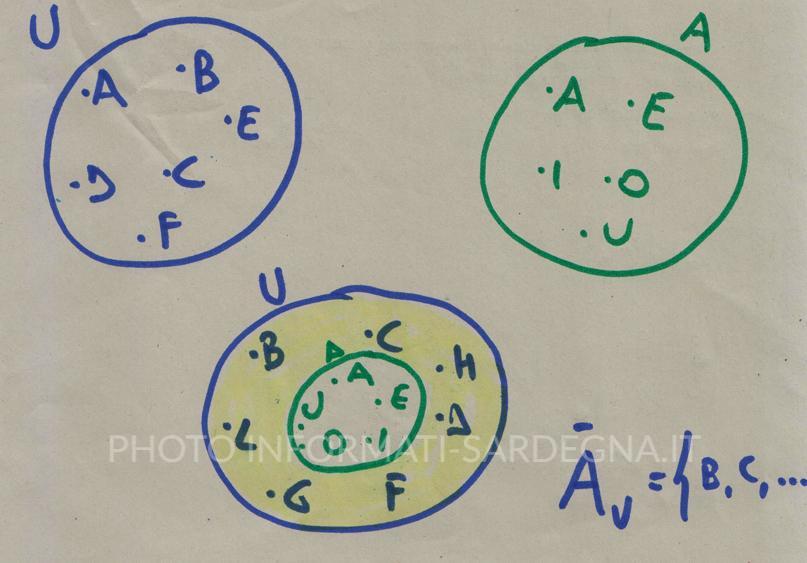
L’insieme complementare è l’insieme degli elementi dell’insieme Universo ( U ) che non appartengono ad A.
- LEGGI ANCHE: Insiemi complementari, esercizi
In italiano la parola “complementare” si usa come aggettivo e indica qualcosa che serve a “complementare”, ovvero a “completare”.
complementare = completare
Rappresentazione dell’insieme complementare
L’insieme complementare si rappresenta con un trattino che sovrasta la lettera maiuscola che denomina l’insieme:


Esempi di insieme complementare



Insieme delle parti
L’Insieme delle parti è l’insieme che ha per elementi tutti i sottoinsiemi.
L’Insieme delle parti si indica col simbolo P(A)
Ad esempio l’insieme A = {1,2,3,4}
L’Insieme delle parti di A è costituito da:
- Insieme proprio dato dai singoli elementi: (1),(2),(3),(4)
- Insieme proprio dato dalle possibili accoppiate di elementi: (1,2); (1,3), (1,4); (2,3), (2,4), (3,4)
- Insieme improprio: A = {1,2,3,4}
- Insieme improprio dell’Insieme vuoto : (∅)
Quindi, scrivendo l’Insieme delle parti di A abbiamo:
- P (A) = {(1,2,3,4)(1),(2),(3),(4)(1,2); (1,3), (1,4); (2,3), (2,4), (3,4)(∅)}
La regola dell’Insieme delle Parti
La regola che permette di mettere in relazione il numero di elementi di A con l’Insieme delle parti di A stesso è la seguente:

Nel caso specifico:
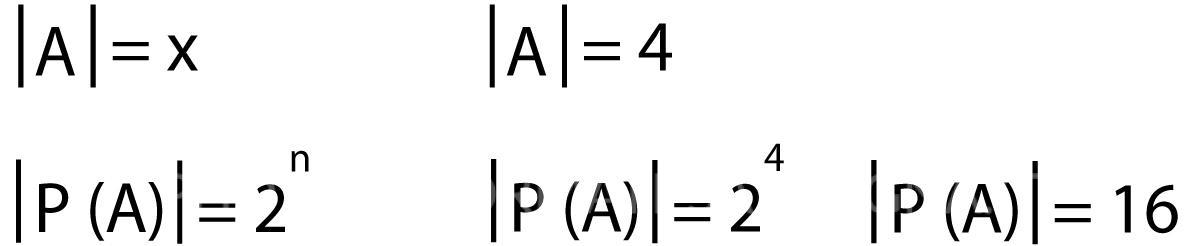
Insieme delle parti
Tutti i sottoinsiemi
Partizione insieme
La partizione dell’insieme è una divisione di dell’insieme in sottoinsiemi, detti parti, tale che non possano esistere parti vuote.
L’unione di tutti i sottoinsiemi costituisce il sovrainsieme di origine.

L’insieme A è costituito dalla partizione dei due sottoinsiemi N e S che riportato in scrittura di elencazione è così esposto: A = {1,2,3,4} ; N = {1,2}; S = {3,4}.
Prodotto cartesiano
Dati due insiemi N e P, il prodotto cartesiano è dato da tutte le coppie ordinate in cui il primo elemento appartiene ad N e il secondo a P. Il prodotto cartesiano si può scrivere nei seguenti modi:
N X P – si legge N per P, oppure N cartesiano P
In simboli:

Ogni singola coppia di elementi è racchiusa tra due parentesi tonde e tra loro sono separati da un punto e virgola. Ovvero: se N è composto dagli elementi a,b,c e P è composto dagli elementi 1,2 il prodotto cartesiano tra i due insiemi viene riportato così: