Teoria degli Insiemi. Soluzioni
- LEGGI ANCHE: Teoria degli Insiemi – Esercizi
Fonte: Matematicamente
Problema 1
Una classe deve svolgere un compito in classe composto da 3 problemi. Il primo problema è risolto da 18 alunni; il secondo problema è risolto da 17 alunni e il terzo problema da 16.
Inoltre 5 studenti hanno risolto sia il primo che il secondo, ma non il terzo. Due hanno risolto il primo e il terzo, ma non il secondo e uno ha risolto tutti i problemi.
Sapendo che tutti hanno risolto almeno un problema, quanti sono gli studenti?
Svolgimento
Dati:
- 3 – compiti in classe da risolvere
- 18 – alunni che risolvono il primo problema
- 17 – alunni che risolvono il secondo problema
- 16 – alunni che risolvono il terzo problema
- 5 – alunni che hanno risolto il primo e il secondo problema
- 2 – alunni che hanno risolto il primo e il terzo problema
- 1 – alunno che ha risolto tutti i problemi
- Tutti – hanno risolto almeno un problema
Quesito: quanti sono gli studenti della classe?
Soluzione:
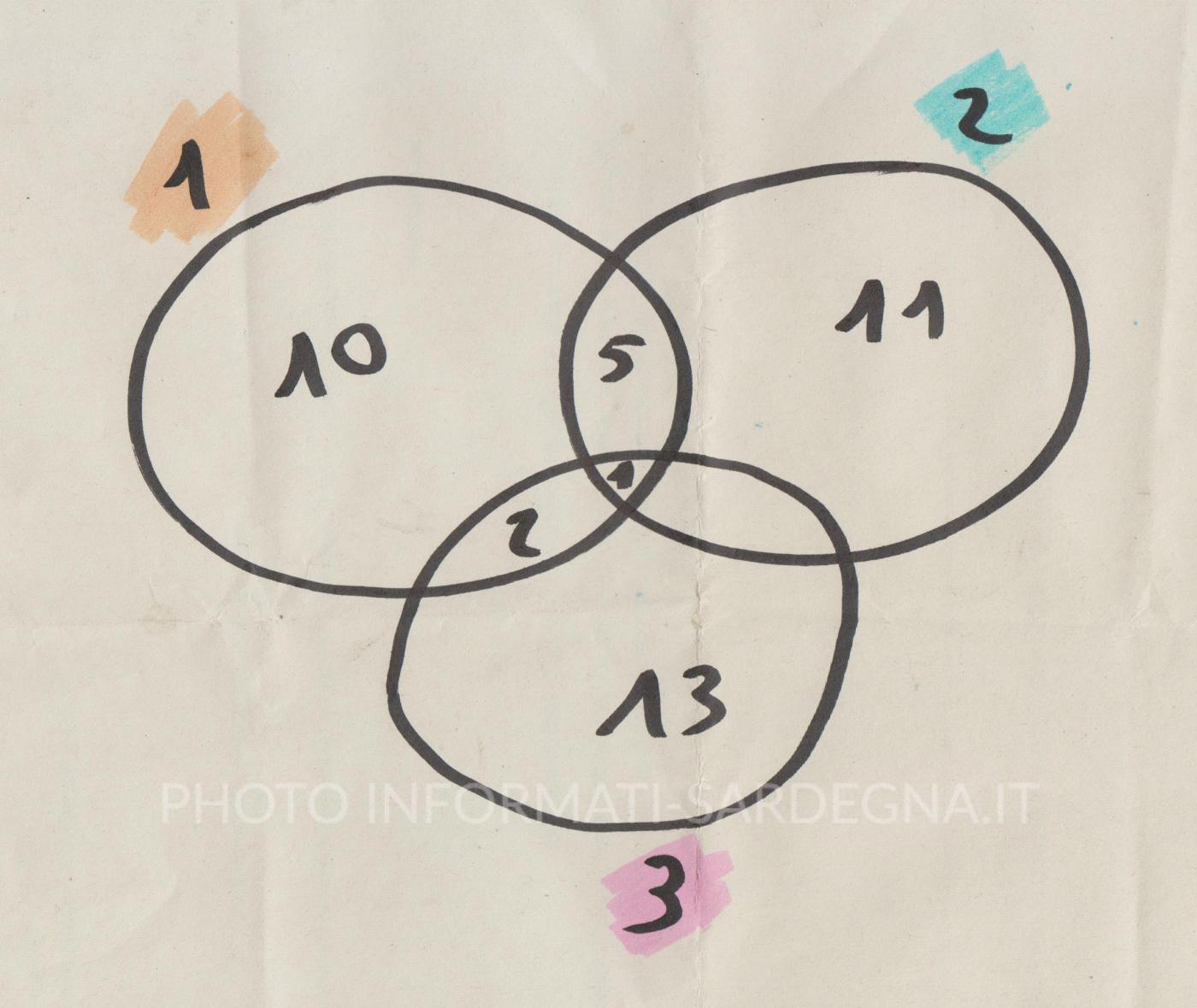
- 10 – alunni che risolvono solo il primo problema
- 5 – alunni che risolvono il primo e il secondo problema
- 11 – alunni che risolvono solo il secondo problema
- 13 – alunni che risolvono solo il terzo problema
- 2 – alunni che risolvono il primo e il terzo problema
- 1 – alunno che risolve tutti i problemi
Totale alunni della classe: 42
Problema 2
Individua i seguenti insiemi:
- A U B
- B ∩ C
- (A U B) U (B ∩ C)
- (A\B)
- (B\A)
- (A\B) U (B\A)
- (AUBUC)
Svolgimento

Problema 3
Sia A l’insieme dei numeri naturali multipli di 5 e minori di 30; B l’insieme dei numeri naturali multipli di 8 e minori di 40 e C, l’insieme dei numeri naturali che sono divisori di 18, determina:
- A ∩ B,
- A ∩ C,
- B ∩ C,
- A U B
- B \ A
Dati:
Insieme A – Insieme dei numeri naturali multipli di 5 e < di 30: 5,10,15,20,25
Insieme B – Insieme dei multipli di 8 e < di 40: 8,16,24,32
Insieme C – Insieme dei numeri naturali divisori di 18: 2,3,6
Quesito: determina le seguenti operazioni insiemistiche
- A ∩ B,
- A ∩ C,
- B ∩ C,
- A U B
- B \ A
Svolgimento
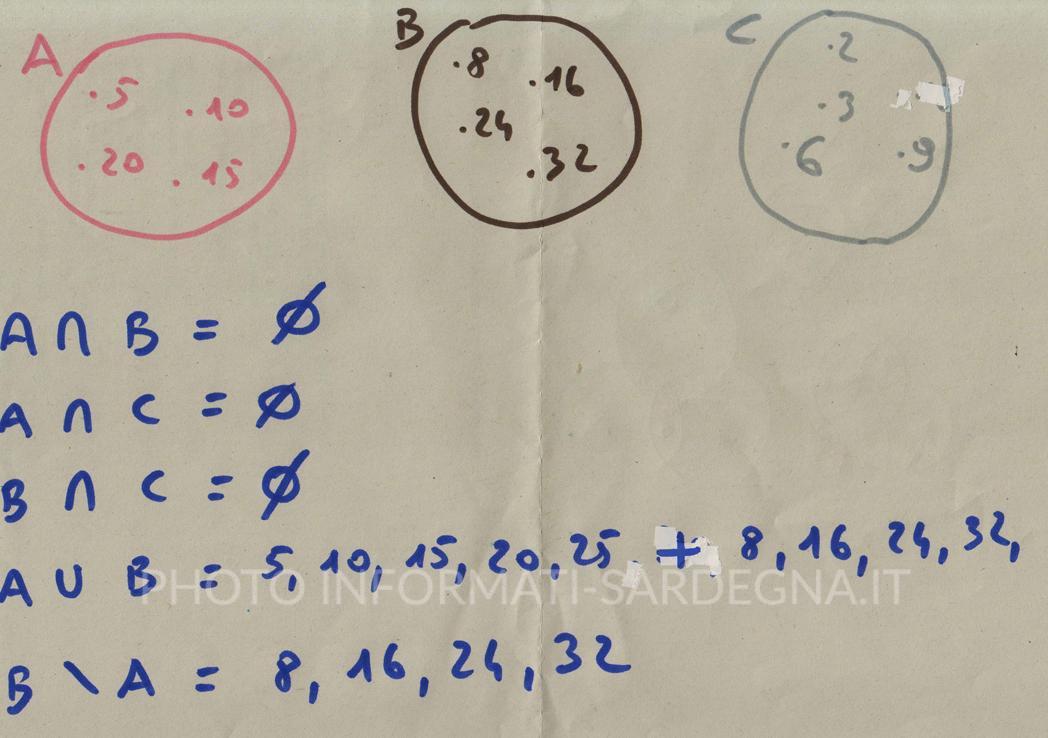
Problema 4
Stabilire le cardinalità dei seguenti insiemi:
A = { x I x ∈ N, x è dispari e x < 20 } – Soluzione: A = {1,3,5,7,9,11,13,15,17,19 } ; A {10 }
B = { x I x ∈ N, x è pari e x < 10 } – Soluzione: B = {2,4,6,8} ; B = {4}
C = { x I x ∈ N, x è pari e x ≤ 10 } – Soluzione: C = {0,2,4,6,8,10} ; B = {6}
Problema 5
Stabilire se A = { x I x ∈ N, x è pari multiplo di 3 } è un sottoinsieme di B = { x I x ∈ N, x è multiplo di 12 }?
Quesito:
Stabilire se A è un sottoinsieme di B
Soluzione:
A = { x I x ∈ N, x è pari multiplo di 3 } ; A = {6,12,24,30… }
B = { x I x ∈ N, x è multiplo di 12 }; B = {12,24, 48… }
A non è un sottoinsieme di B
Problema 6
Calcolare l’insieme delle parti di A = { 2,3,6 } e stabilire, senza determinarlo, le cardinalità dell’insieme della parti di B = {1,2,3,4,5,6,7,8,9,10}.
Svolgimento
L’insieme delle parti di A:
- Insieme improprio A ={ 2,3,6 }
- Insieme improprio Insieme vuoto A = {Ø}
- Insieme proprio dato dai singoli elementi presi una volta A = {2}, {3}, {6}
- Insieme proprio dato da tutti i possibili accomppiamenti degli elementi: A = {2,3}; {2,6};{3,6}; {2}; {3}; {6}.
Ovvero:
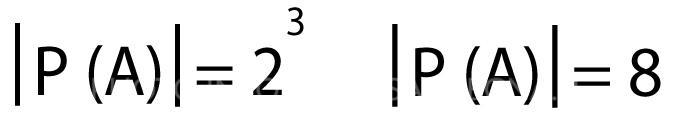
Cardinalità dell’insieme delle parti di B (cioè contare quanti insiemi sono contenuti in B) B = {1,2,3,4,5,6,7,8,9,10}:
- 10 – {1,2,3,4,5,6,7,8,9,10} +
- 9 – (1,2); (1,3); (1,4); (1,5); (1,6); (1,7); (1,8) ; (1,9) ; (1,10} +
- 8 – (2,3); (2,4); (2,5); (2,6); (2,7); (2,8) ; (2,9) ; (2,10} +
- 7 – (3,4); (3,5); (3,6); (3,7); (3,8) ; (3,9) ; (3,10} +
- 6 – (4,5); (4,6); (4,7); (4,8) ; (4,9) ; (4,10} +
- 5 – (5,6); (5,7); (5,8) ; (5,9) ; (5,10} +
- 4 – (6,7); (6,8) ; (6,9) ; (6,10} +
- 3 – (7,8) ; (7,9) ; (7,10} +
- 2 – (2,9) ; (2,10} +
- 1 – (∅)
Cardinalità dell’Insieme delle parti di B:
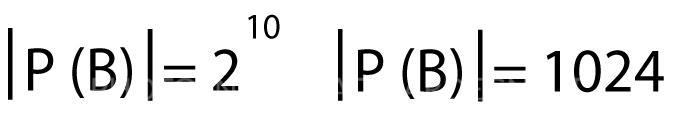
Fonte: Daniele Baldissin
Problema 7
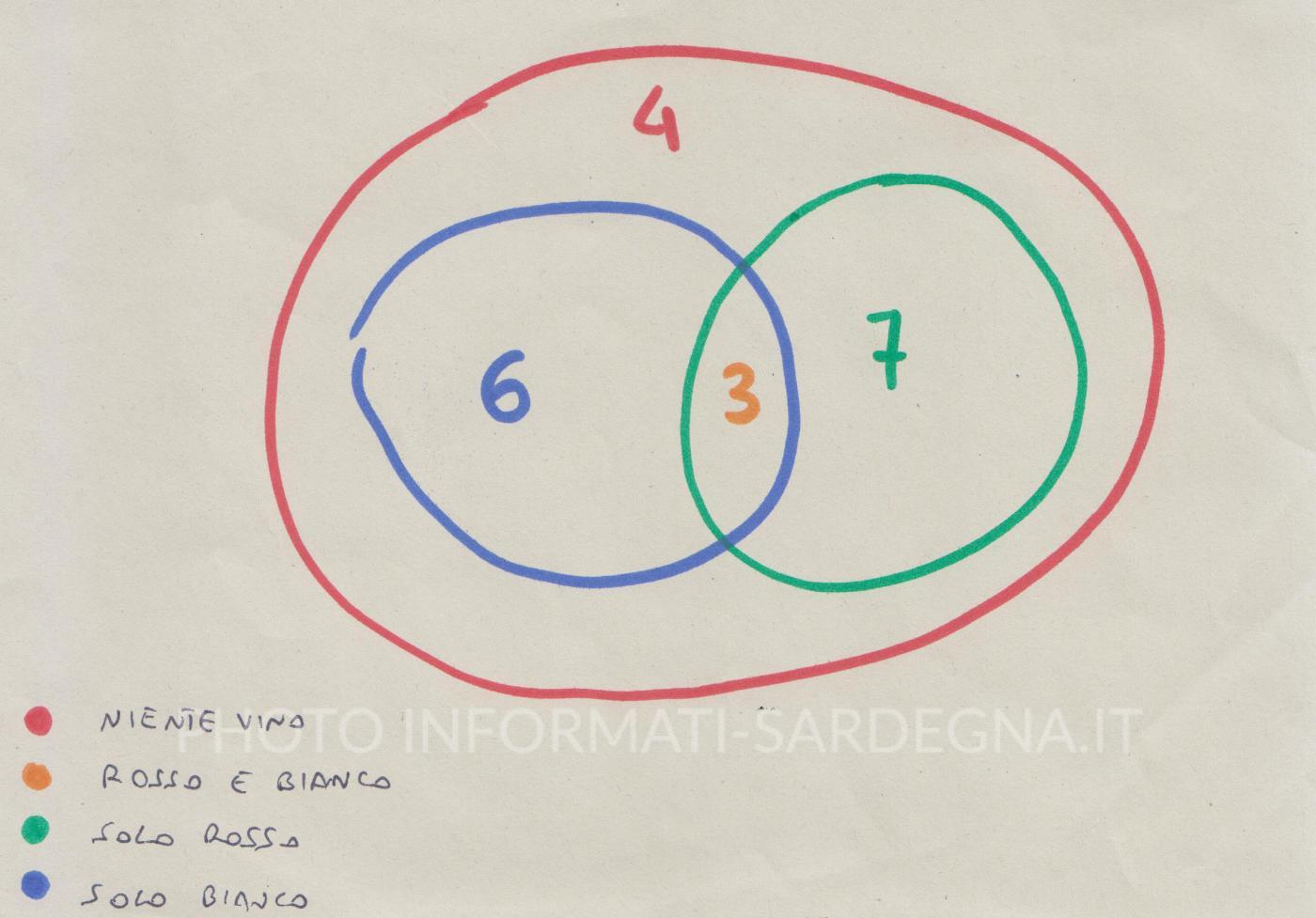
Ad una festa di compleanno partecipano 20 persone. Di queste 9 bevono vino bianco, 10 rosso e 3 sia bianco che rosso. Visualizza la situazione descritta e calcola quante persone non hanno bevuto ne bianco ne rosso.
Dati:
- 20 – invitati al compleanno
- 9 – invitati che bevono vino bianco
- 10 – invitati che bevono vino rosso
- 3 – invitati che bevono rosso e bianco
Quesito: quante persone non hanno bevuto ne bianco ne rosso?
Svolgimento
Problema 8
In una scuola frequentano 200 alunni, la maggior parte di essi ha trascorso le vacanze al mare e in montagna. In particolare si ha che:
- 115 hanno trascorso le vacanze al mare
- 35 hanno trascorso le vacanze sia al mare che in montagna
- 25 non ha fatto alcuna vacanza
Quesito: quanti sono gli alunni che hanno trascorso le vacanze solo in montagna?
Svolgimento

Problema 9
Una scuola organizza due corsi di recupero: quello di inglese a cui partecipano 30 studenti e quello di matematica a cui partecipano 36 studenti. Quanti alunni in totale partecipano sapendo che i corsi si tengono in orari diversi e che 16 alunni frequentano entrambi i corsi?
Dati:
- 2 – corsi di recupero organizzati dalla scuola
- 30 – numero di studenti che partecipano al corso di Inglese
- 36 – numero di studenti che partecipano al corso di matematica
- 16 – numero di studenti che partecipano a entrambi i corsi
Quesito: quanti studenti partecipano ai corsi?
Svolgimento

Problema 10
Da un’indagine condotta in una classe di 25 alunni sul tipo di sport che preferiscono fare i ragazzi, risulta che 12 hanno scelto il calcio, 11 la pallacanestro e 8 la pallavolo.
Si sà inoltre che 2 amano le 3 discipline, 3 solo il calcio e la pallacanestro, 2 solo la pallacanestro e la pallavolo.
Calcola gli alunni che preferiscono pallavolo e calcio
Dati:
- 25 – numero di alunni della classe
- 12 – alunni che preferiscono il calcio
- 11 – alunni che preferiscono la pallacanestro
- 8 – alunni che preferiscono la pallavolo
- 2 – alunni che preferiscono tutte e tre le discipline
- 3 – alunni che amano solo il calcio e la pallacanestro
- 2 – alunni che amano solo la pallacanestro e la pallavolo
Svolgimento:

Problema 11
Una indagine condotta su 26 alunni ha stabilito che la mattina tutti i ragazzi fanno colazione e che 15 di loro bevono latte, 6 latte e caffè e 8 solo thè. Domanda, quanti bevono solo caffè?
Dati:
- 26 – gli alunni che sono stati oggetto dell’indagine
- 15 – alunni che bevono latte
- 6 – alunni che bevono latte e caffè
- 8 – alunni che bevono solo thè
Quesito: quanti alunni bevono solo caffè?
Svolgimento









