Definizione
La circonferenza è l’insieme dei punti di un piano, aventi tutti la stessa distanza da un punto chiamato centro.
La distanza tra un punto qualsiasi della circonferenza e il centro si chiama raggio.
La circonferenza è una linea; il cerchio è una superficie.
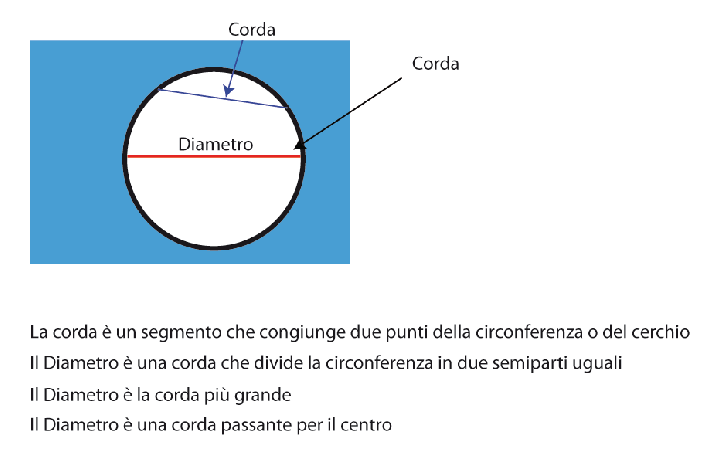
LA CORDA
Ogni segmento che congiunge due punti della circonferenza si chiama corda
La corda passante per il centro prende il nome di diametro.

La perpendicolare, condotta dal centro di una circonferenza ad una corda, divide la corda in due parti uguali;
- corde uguali di una stessa circonferenza hanno uguali distanze dal centro → viceversa → corde che hanno uguale distanza dal centro sono uguali
- alla corda maggiore corrisponde minore distanza dal centro
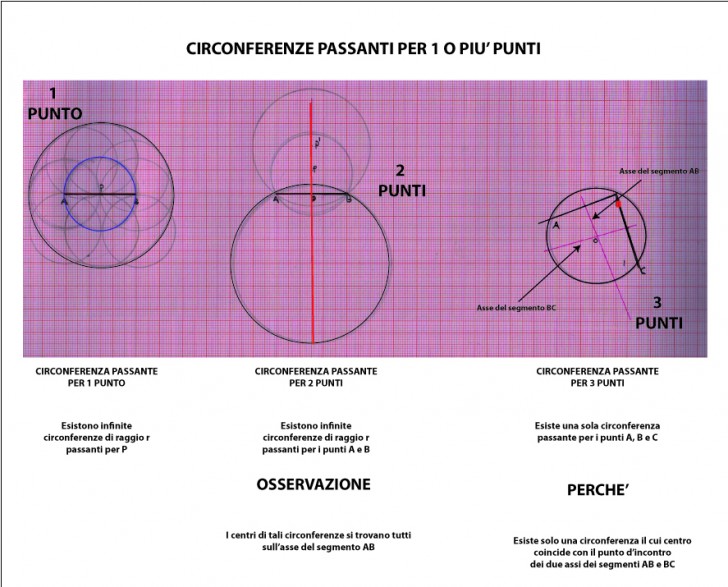
CIRCONFERENZE PASSANTI PER UNO O PIU’ PUNTI
– Esistono infinite circonferenze di raggio r passanti per P
– Esistono infinite circonferenze passanti contemporaneamente per due punti A e B(Fig.2). Quindi esistono infinite circonferenze per due punti assegnati
– Esiste una ed una sola circonferenza passante per tre punti assegnati (Fig.3). Questo perchè gli assi dei segmenti AB e BC (che sono due corde) si incontrano in un solo punto O, che è l’unico punto del piano ad essere equidistante dai tre punti dati.
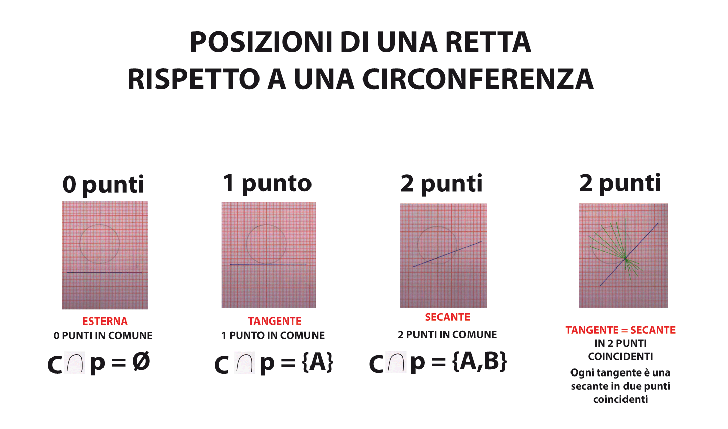
POSIZIONI DI UNA RETTA RISPETTO A UNA CIRCONFERENZA
Date in un piano una retta p e una circonferenza C, possono presentarsi tre situazioni:
1) La retta e la circonferenza hanno in comune due punti (A e B); cioè C intersezione p = {A, B} → retta secante
2) La retta e la circonferenza hanno in comune un solo punto A detto punto di tangenza; cioè C intersezione p = {A} → retta tangente
3) La retta e la circonferenza non hanno punti in comune; cioè C intersezione p = à˜ → retta esterna
Dalle suddette condizioni si ricava che:
1) La distanza dal centro della circonferenza di una secante è minore del raggio;
2) La distanza di una retta tangente è uguale al raggio;
3) La distanza di una retta esterna è maggiore del raggio.
Viceversa:
1) Una retta che ha dal centro una distanza minore del raggio è definita secante;
2) Una retta che ha dal centro una distanza uguale al raggio è definita tangente;
3) Una retta che ha dal centro una maggiore distanza del raggio è definita esterna
4) Una retta tangente può essere una secante in due punti coincidenti. Una retta s che secante nei punti A e B, se la facciamo ruotare lungo la circonferenza in un senso o nell’altro, incontrerà la stessa nei punti C,D,E… fino a coincidere col punto A.
POSIZIONI RECIPROCHE DI DUE CIRCONFERENZE
Date in un piano due circonferenze C e C’, può presentarsi una delle seguenti situazioni:
– Le due circonferenze sono secanti
– Le due circonferenze sono tangenti: tangenti interne e tangenti esterne
– Le due circonferenze non hanno alcun punto in comune: le due circonferenze sono esterne o interne
 PARTI DELLA CIRCONFERENZA
PARTI DELLA CIRCONFERENZA
E DEL CERCHIO
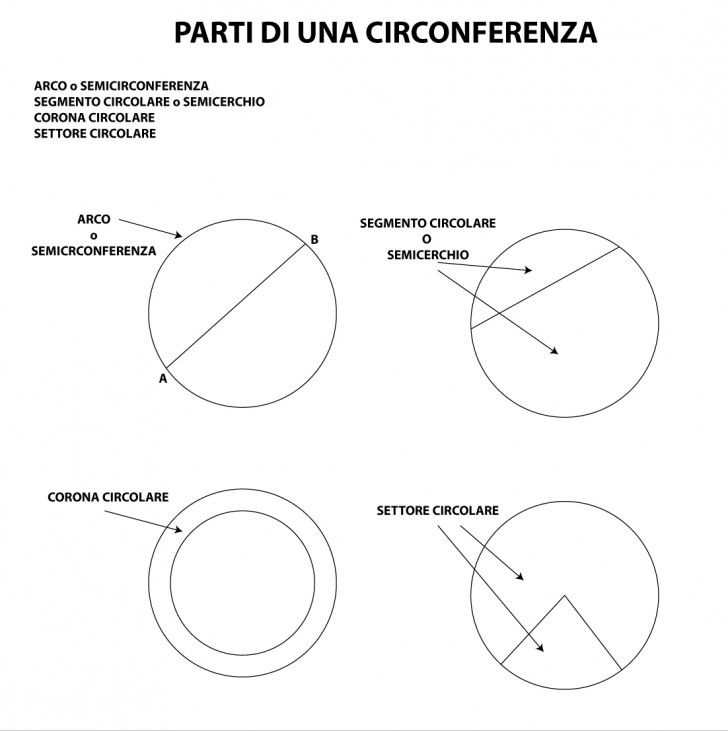
Sono parti di una circonferenza:
- L’arco
- Il segmento circolare (o semicerchio)
- La corona circolare
- Il settore circolare
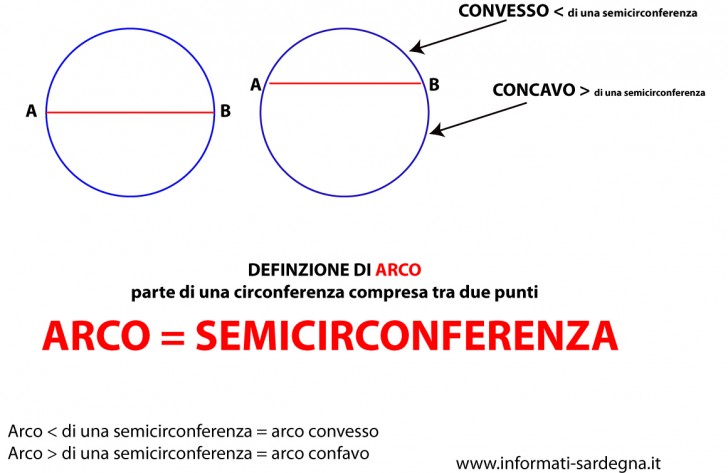
Due punti A e B dividono una circonferenza in due parti, ciascuna delle quali si chiama arco.
– Semicirconferenze – quando i due punti A e B sono gli estremi di un diametro;
– Archi convessi – quando gli archi sono minori di una semicirconferenza
– Archi concavi – quando gli archi sono maggiori di una semicirconferenza
IL SEGMENTO CIRCOLARE
Una corda divide un cerchio in due parti, ciascuna delle quali si chiama segmento circolare (o semicerchio).
Differenza tra semicirconferenza e semicerchio:
– La circonferenza è una linea circolare
– Il cerchio è una superficie circolare
– Un arco è una semicirconferenza sottesa tra due punti A e B
– Un segmento circolare è un semicerchio avente come base una corda

CORONA CIRCOLARE
Due circonferenze distinte aventi lo stesso centro si dicono concentriche. La parte di piano compresa fra due circonferenze concentriche si chiama settore circolare.
SETTORE CIRCOLARE
Il settore circolare è ognuna delle parti in cui un cerchio resta diviso da due raggi. Se i due raggi sono diametralmente opposti i due settori sono semicerchi.
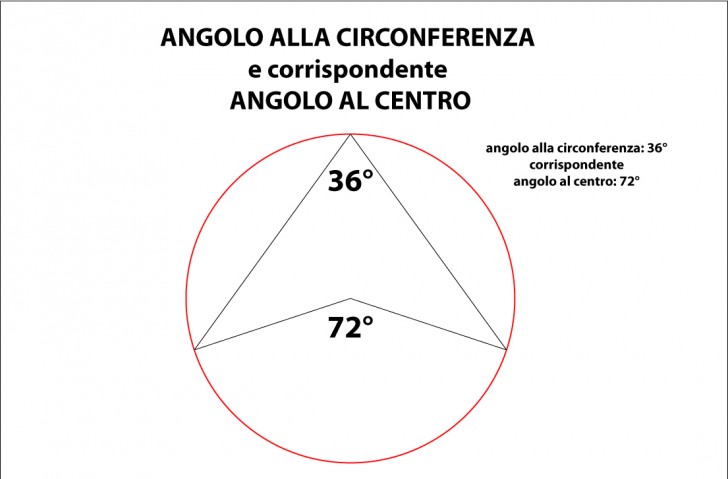
ANGOLI AL CENTRO E ANGOLI ALLA CIRCONFERENZA
- Gli angoli al centro hanno il vertice nel centro O della circonferenza
- Gli angoli alla circonferenza hanno il vertice nella traccia della circonferenza
Gli angoli alla circonferenza sono la metà dei corrispondenti angoli al centro (figura)
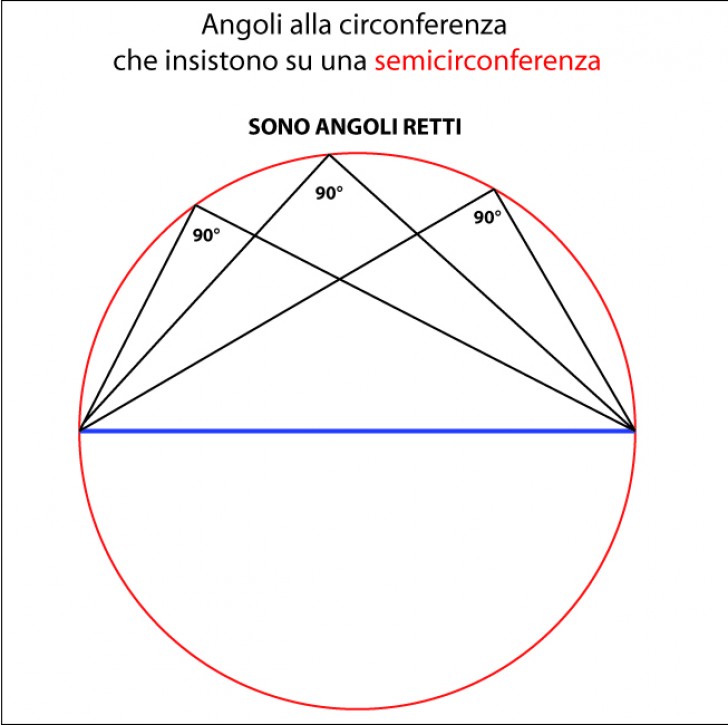
Caratteristiche degli angoli alla circonferenza:
– Tutti gli angoli alla circonferenza che insistono su un medesimo arco, sono uguali tra loro
– Tutti gli angoli alla circonferenza inscritti in una semcirconferenza sono angoli retti (figura)
SIMMETRIA DEL CERCHIO
Il cerchio e la circonferenza hanno un infinito numero infinito di assi di simmetria
Il cerchio e la circonferenza possiedono, come assi di simmetria, un fascio di rette il cui centro è il centro stesso del cerchio.
Nessun’altra figura geometrica piana regolare dispone di un numero infinito di assi di simmetria
– Il trapezio rettangolo ha 0 assi di simmetria
– Il triangolo rettangolo ha 0 assi di simmetria
– Il triangolo isoscele ha 3 assi di simmetria
– Il quadrato ha 4 assi di simmetria
– Il pentagono ha 5 assi di simmetria
– L’esagono ha 6 assi di simmetria
Autore articolo: Pierpaolo Spanu
Foto di copertina: Vivek Doshi on Unsplash








































